
【题目】已知数列![]() 满足
满足![]() ,
,![]() ,我们知道当a取不同的值时,得到不同的数列.如当
,我们知道当a取不同的值时,得到不同的数列.如当![]() 时,得到无穷数列:0,
时,得到无穷数列:0,![]() ,
,![]() ,
,![]() ,…,当
,…,当![]() 时,得到有穷数列:
时,得到有穷数列:![]() ,
,![]() ,1.
,1.
(1)当a为何值时,![]() ;
;
(2)设数列![]() 满足
满足![]() ,
,![]() ,求证:a取
,求证:a取![]() 中的任一数,都可以得到一个有穷数列
中的任一数,都可以得到一个有穷数列![]() ;
;
(3)是否存在实数a,使得到的![]() 是无穷数列,且对于任意
是无穷数列,且对于任意![]() ,都有
,都有![]() 成立,若存在,求出a的取值范围;若不存在,请说明理由.
成立,若存在,求出a的取值范围;若不存在,请说明理由.
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴建立极坐标系.已知曲线
轴正半轴为极轴建立极坐标系.已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,射线
,射线![]() 与曲线
与曲线![]() 交于点
交于点![]() ,点
,点![]() 满足
满足![]() ,设倾斜角为
,设倾斜角为![]() 的直线
的直线![]() 经过点
经过点![]() .
.
(1)求曲线![]() 的直角坐标方程及直线
的直角坐标方程及直线![]() 的参数方程;
的参数方程;
(2)直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点,当
两点,当![]() 为何值时,
为何值时,![]() 最大?求出此最大值.
最大?求出此最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥A-BCD中,平面ABC丄平面ADC, AD丄AC,AD=AC, ![]() ,若此三棱锥的外接球表面积为
,若此三棱锥的外接球表面积为![]() ,则三棱锥A-BCD体积的最大值为( )
,则三棱锥A-BCD体积的最大值为( )
A.7B.12C.6D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() .
.
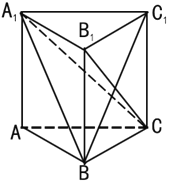
(1)求证:![]() 平面
平面![]() ;
;
(2)求异面直线![]() 与
与![]() 所成角的大小;
所成角的大小;
(3)点![]() 在线段
在线段![]() 上,且
上,且![]() ,点
,点![]() 在线段
在线段![]() 上,若
上,若![]() 平面
平面![]() ,求
,求![]() 的值(用含
的值(用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,射线
中,射线![]() 的方程为
的方程为![]() ,以坐标原点
,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的方程为
的方程为![]() .一只小虫从点
.一只小虫从点![]() 沿射线
沿射线![]() 向上以
向上以![]() 单位/min的速度爬行
单位/min的速度爬行
(1)以小虫爬行时间![]() 为参数,写出射线
为参数,写出射线![]() 的参数方程;
的参数方程;
(2)求小虫在曲线![]() 内部逗留的时间.
内部逗留的时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,的焦点为
,的焦点为![]() ,过点
,过点![]() 的直线
的直线![]() 的斜率为
的斜率为![]() ,与抛物线
,与抛物线![]() 交于
交于![]() ,
,![]() 两点,抛物线在点
两点,抛物线在点![]() ,
,![]() 处的切线分别为
处的切线分别为![]() ,
,![]() ,两条切线的交点为
,两条切线的交点为![]() .
.
(1)证明:![]() ;
;
(2)若![]() 的外接圆
的外接圆![]() 与抛物线
与抛物线![]() 有四个不同的交点,求直线
有四个不同的交点,求直线![]() 的斜率的取值范围.
的斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某土特产超市为预估2020年元旦期间游客购买土特产的情况,对2019年元旦期间的90位游客购买情况进行统计,得到如下人数分布表.
购买金额(元) |
|
|
|
|
|
|
人数 | 10 | 15 | 20 | 15 | 20 | 10 |
(1)根据以上数据完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为购买金额是否少于60元与性别有关.
的把握认为购买金额是否少于60元与性别有关.
不少于60元 | 少于60元 | 合计 | |
男 | 40 | ||
女 | 18 | ||
合计 |
(2)为吸引游客,该超市推出一种优惠方案,购买金额不少于60元可抽奖3次,每次中奖概率为![]() (每次抽奖互不影响,且
(每次抽奖互不影响,且![]() 的值等于人数分布表中购买金额不少于60元的频率),中奖1次减5元,中奖2次减10元,中奖3次减15元.若游客甲计划购买80元的土特产,请列出实际付款数
的值等于人数分布表中购买金额不少于60元的频率),中奖1次减5元,中奖2次减10元,中奖3次减15元.若游客甲计划购买80元的土特产,请列出实际付款数![]() (元)的分布列并求其数学期望.
(元)的分布列并求其数学期望.
附:参考公式和数据: ,
,![]() .
.
附表:
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 |
| 0.150 | 0.100 | 0.050 | 0.010 | 0.005 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com