
【题目】已知函数![]() ,
, ![]() ,(其中
,(其中![]() ,
, ![]() 为自然对数的底数,
为自然对数的底数, ![]() ……).
……).
(1)令![]() ,若
,若![]() 对任意的
对任意的![]() 恒成立,求实数
恒成立,求实数![]() 的值;
的值;
(2)在(1)的条件下,设![]() 为整数,且对于任意正整数
为整数,且对于任意正整数![]() ,
, ![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)1;(2)2
【解析】试题分析:(1)求出函数的导数,求出h(x)的解析式,求出函数的导数,通过讨论a的范围,求出函数的单调区间,从而求出函数的最小值,求出a的值即可;(2)得到1+x≤ex,令x=﹣![]() (n∈N*,k=0,1,2,3,…,n﹣1),则0<1﹣
(n∈N*,k=0,1,2,3,…,n﹣1),则0<1﹣![]() ≤
≤![]() ,得到
,得到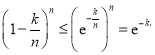 累加,通过放大不等式,证明即可.
累加,通过放大不等式,证明即可.
解析:
(1)因为![]() ,所以
,所以![]() ,
,
由![]() 对任意的
对任意的![]() 恒成立,即
恒成立,即![]() ,由
,由![]() ,
,
(i)当![]() 时,
时, ![]() ,
, ![]() 的单调递增区间为
的单调递增区间为![]() ,
,
所以![]() 时,
时, ![]() ,所以不满足题意.
,所以不满足题意.
(ii)当![]() 时,由
时,由![]() ,得
,得![]()
![]() 时,
时, ![]() ,
, ![]() 时,
时, ![]() ,
,
所以![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,
上单调递增,
所以![]() 的最小值为
的最小值为![]() .
.
设![]() ,所以
,所以![]() ,① 因为
,① 因为![]() ,令
,令![]() 得
得![]() ,所以
,所以![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减,
上单调递减,
所以![]() ,②,由①②得
,②,由①②得![]() ,则
,则![]() .
.
(2)由(1)知![]() ,即
,即![]() ,
,
令![]() (
(![]() ,
, ![]() )则
)则![]() ,
,
所以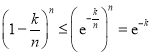 ,
,
所以![]()
![]() ,
,
所以![]() ,又
,又![]() ,所以
,所以![]() 的最小值为
的最小值为![]()


科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为F,直线
的焦点为F,直线![]() 与x轴的交点为P,与抛物线的交点为Q,且
与x轴的交点为P,与抛物线的交点为Q,且![]() .
.
(1)求抛物线的方程;
(2)过F的直线l与抛物线相交于A,D两点,与圆![]() 相交于B,C两点(A,B两点相邻),过A,D两点分别作抛物线的切线,两条切线相交于点M,求△ABM与△CDM的面积之积的最小值.
相交于B,C两点(A,B两点相邻),过A,D两点分别作抛物线的切线,两条切线相交于点M,求△ABM与△CDM的面积之积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了鼓励学生热心公益,服务社会,成立了“慈善义工社”.2017年12月,该校“慈善义工社”为学生提供了4次参加公益活动的机会,学生可通过网路平台报名参加活动.为了解学生实际参加这4次活动的情况,该校随机抽取100名学生进行调查,数据统计如下表,其中“√”表示参加,“×”表示未参加.
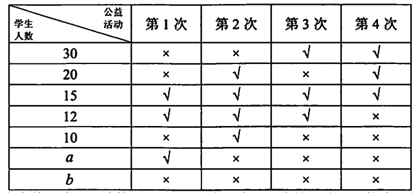
根据表中数据估计,该校4000名学生中约有120名这4次活动均未参加.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)从该校4000名学生中任取一人,试估计其2017年12月恰参加了2次学校组织的公益活动的概率;
(Ⅲ)已知学生每次参加公益活动可获得10个公益积分,任取该校一名学生,记该生2017年12月获得的公益积分为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在(0,+∞)上的单调函数f(x),x∈(0,+∞),f[f(x)﹣lnx]=1,则方程f(x)﹣f′(x)=1的解所在区间是 ( )
A. (2,3) B. ![]() C.
C. ![]() D. (1,2)
D. (1,2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)=sin2ax-![]() sin ax·cos ax-
sin ax·cos ax-![]() (a>0)的图象与直线y=b相切,并且切点的横坐标依次成公差为
(a>0)的图象与直线y=b相切,并且切点的横坐标依次成公差为![]() 的等差数列.
的等差数列.
(1)求a,b的值;
(2)若x0∈![]() ,且x0是y=f(x)的零点,试写出函数y=f(x)在
,且x0是y=f(x)的零点,试写出函数y=f(x)在![]() 上的单调增区间.
上的单调增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在[1,+∞)上的函数f(x)满足:①f(2x)=2f(x);②当2≤x≤4时,f(x)=1-|x-3|.则函数g(x)=f(x)-2在区间[1,28]上的零点个数为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com