
已知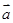 =(2,1),
=(2,1),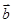 =(-3,4),则3
=(-3,4),则3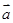 +4
+4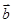 = .
= .
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源:河南省卫辉市第一中学2012届高三4月考试数学理科试题 题型:047
已知|x1-2|<1,|x2-2|<1.
(Ⅰ)求证:2<x1+x2<6,|x1-x2|=2;
(Ⅱ)若f(x)=x2-x+1,求证:|x1-x2|<|f(x1)-f(x2)|<5|x1-x2|.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分14分)
在△OAB的边OA,OB上分别有一点P,Q,已知![]() :
:![]() =1:2,
=1:2, ![]() :
:![]() =3:2,连结AQ,BP,设它们交于点R,若
=3:2,连结AQ,BP,设它们交于点R,若![]() =a,
=a,![]() =b.
=b.
(1)用a与 b表示![]() ;
;
(2)过R作RH⊥AB,垂足为H,若| a|=1, | b|=2, a与 b的夹角![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014届广东省高一期中考试文科数学试卷A卷(解析版) 题型:解答题
已知函数f(x)(x∈R)满足f(x)= ,a≠0,f(1)=1,且使f(x)=2x成立的实数x只有一个.
,a≠0,f(1)=1,且使f(x)=2x成立的实数x只有一个.
(1)求函数f(x)的表达式;
(2)若数列{an}满足a1= ,an+1=f(an),bn=
,an+1=f(an),bn= -1,n∈N*,证明数列{bn}是等比数列,并求出{bn}的通项公式;
-1,n∈N*,证明数列{bn}是等比数列,并求出{bn}的通项公式;
(3)在(2)的条件下,证明:a1b1+a2b2+…+anbn<1(n∈N*).
【解析】解: (1)由f(x)= ,f(1)=1,得a=2b+1.
,f(1)=1,得a=2b+1.
由f(x)=2x只有一解,即 =2x,
=2x,
也就是2ax2-2(1+b)x=0(a≠0)只有一解,
∴b=-1.∴a=-1.故f(x)= .…………………………………………4分
.…………………………………………4分
(2)an+1=f(an)= (n∈N*),bn=
(n∈N*),bn= -1, ∴
-1, ∴ =
= =
= =
= ,
,
∴{bn}为等比数列,q= .又∵a1=
.又∵a1= ,∴b1=
,∴b1= -1=
-1= ,
,
bn=b1qn-1=
 n-1=
n-1= n(n∈N*).……………………………9分
n(n∈N*).……………………………9分
(3)证明:∵anbn=an =1-an=1-
=1-an=1- =
= ,
,
∴a1b1+a2b2+…+anbn= +
+ +…+
+…+ <
< +
+ +…+
+…+
= =1-
=1- <1(n∈N*).
<1(n∈N*).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com