
����Ŀ�����һ�����дӵ�2����ÿһ������ǰһ��IJ����2������������Ϊ��H�����С���
��1��������{an}Ϊ��H�����С�����a1= ![]() ��3��a2=
��3��a2= ![]() ��a3=4����ʵ��m��ȡֵ��Χ��
��a3=4����ʵ��m��ȡֵ��Χ��
��2���Ƿ��������Ϊ1�ĵȲ�����{an}Ϊ��H�����С�������ǰn���Sn����Sn��n2+n��n��N*���������ڣ������{an}��ͨ�ʽ���������ڣ���˵�����ɣ�
��3����֪�ȱ�����{an}��ÿһ���Ϊ����������{an}Ϊ��H�����С���bn= ![]() an �� cn=
an �� cn= ![]() ��������{bn}���ǡ�H�����С�ʱ�����ж�����{cn}�Ƿ�Ϊ��H�����С�����˵�����ɣ�
��������{bn}���ǡ�H�����С�ʱ�����ж�����{cn}�Ƿ�Ϊ��H�����С�����˵�����ɣ�
���𰸡�
��1���⣺������ã�a2��a1=3��2��a3��a2=4�� ![]() ��2����2��
��2����2�� ![]() =
= ![]() ��0�����m
��0�����m ![]() ��m��0��
��m��0��
��ʵ��m��ȡֵ��Χʱ�����ޣ�0���� ![]()
��2���⣺������ڵȲ�����{an}Ϊ��H�����С����蹫��Ϊd����d��2����a1=1���ɵã�Sn=n+ ![]() ��������ɵã�n+
��������ɵã�n+ ![]() ��n2+n��n��N*����������d
��n2+n��n��N*����������d ![]() ����������
���������� ![]() =2+
=2+ ![]() ��2����
��2���� ![]()
![]() =2����d��2����d��2ì�ܣ���˲����ڵȲ�����{an}Ϊ��H�����С�
=2����d��2����d��2ì�ܣ���˲����ڵȲ�����{an}Ϊ��H�����С�
��3���⣺��ȱ�����{an}�Ĺ���Ϊq����an= ![]() ����ÿһ���Ϊ����������an+1��an=an��q��1����2��0��
����ÿһ���Ϊ����������an+1��an=an��q��1����2��0��
��a1��0��q��1����an+1��an=an��q��1����an��an��1����������{an��an��1}��n��2���У���a2��a1��Ϊ��С�
ͬ��������{bn��bn��1}��n��2���У���b2��b1��Ϊ��С���{an}Ϊ��H�����С�����ֻ֪��a2��a1��2��
�� a1��q��1����2������Ϊ{bn}���ǡ�H�����С����ҡ�b2��b1��Ϊ��С���b2��b1��2���� a1��q��1����3
��������{an}��ÿһ���Ϊ���������ɵ� a1��q��1��=3����a1=1��q=4��a1=3��q=2��
�ٵ�a1=1��q=4ʱ�� ![]() ����
���� ![]() ����
���� ![]() ����
���� ![]() ����
���� ![]() ����
���� ![]()
= ![]() ��
��
��{dn}Ϊ�������У�
�� dn��dn��1��dn��2������d1��
�� cn+1��cn��cn��cn��1��cn��1��cn��2������c2��c1��
�� ![]() �����ԣ��������n��N*����cn+1��cn��2��
�����ԣ��������n��N*����cn+1��cn��2��
������{cn}Ϊ��H�����С����ڵ�a1=3��q=2ʱ�� ![]() ��
��
�� ![]() ����Ȼ��{cn}Ϊ�ݼ����У�c2��c1��0��2��
����Ȼ��{cn}Ϊ�ݼ����У�c2��c1��0��2��
������{cn}���ǡ�H�����С���
���ϣ��� ![]() ʱ������{cn}Ϊ��H�����С���
ʱ������{cn}Ϊ��H�����С���
�� ![]() ʱ������{cn}���ǡ�H�����С�
ʱ������{cn}���ǡ�H�����С�
����������1��������ã�a2��a1=3��2��a3��a2=4�� ![]() ��2����2��
��2����2�� ![]() =
= ![]() ��0�����m��Χ���ɵó�����2��������ڵȲ�����{an}Ϊ��H�����С����蹫��Ϊd����d��2����a1=1���ɵã�Sn=n+
��0�����m��Χ���ɵó�����2��������ڵȲ�����{an}Ϊ��H�����С����蹫��Ϊd����d��2����a1=1���ɵã�Sn=n+ ![]() ��������ɵã�n+
��������ɵã�n+ ![]() ��n2+n��n��N*����������d
��n2+n��n��N*����������d ![]() ����������������жϳ����ۣ���3����ȱ�����{an}�Ĺ���Ϊq����an=
����������������жϳ����ۣ���3����ȱ�����{an}�Ĺ���Ϊq����an= ![]() ����ÿһ���Ϊ����������an+1��an=an��q��1����2��0���ɵ�an+1��an=an��q��1����an��an��1 �� ��������{an��an��1}��n��2���У���a2��a1��Ϊ��С�ͬ��������{bn��bn��1}��n��2���У���b2��b1��Ϊ��С���{an}Ϊ��H�����С�����ֻ֪��a2��a1��2���� a1��q��1����2������Ϊ{bn}���ǡ�H�����С����ҡ�b2��b1��Ϊ��С��ɵ�b2��b1��2���� a1��q��1����3��������{an}��ÿһ���Ϊ���������ɵ� a1��q��1��=3��a1=1��q=4��a1=3��q=2��ͨ���������ۼ����жϳ����ۣ�
����ÿһ���Ϊ����������an+1��an=an��q��1����2��0���ɵ�an+1��an=an��q��1����an��an��1 �� ��������{an��an��1}��n��2���У���a2��a1��Ϊ��С�ͬ��������{bn��bn��1}��n��2���У���b2��b1��Ϊ��С���{an}Ϊ��H�����С�����ֻ֪��a2��a1��2���� a1��q��1����2������Ϊ{bn}���ǡ�H�����С����ҡ�b2��b1��Ϊ��С��ɵ�b2��b1��2���� a1��q��1����3��������{an}��ÿһ���Ϊ���������ɵ� a1��q��1��=3��a1=1��q=4��a1=3��q=2��ͨ���������ۼ����жϳ����ۣ�
�����㾫����������Ĺؼ������������е�ǰn��͵����֪ʶ����������{an}��ǰn���sn��ͨ��an�Ĺ�ϵ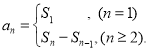 ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��=|3x��1|+x+2��
��1���ⲻ��ʽf��x����3��
��2��������ʽf��x����a�Ľ⼯ΪR����a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a�dz�����������ʵ��x������ʽ|x+1|��|2��x|��a��|x+1|+|2��x|��������
������a��ֵ��
������m��n��0����֤��2m+ ![]() ��2n+a��
��2n+a��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]() ��
��
��1����f��x�������ݼ����䣻
��2����֪��ABC�У�����sin2B+sin2C��sinBsinC+sin2A����f��A����ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}����a1=1��a2=3����|an+1��an|=2n��n��N*������{a2n��1}�ǵ������С�{a2n}�ǵݼ����У��� ![]()
![]() = ��
= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ��ʾ��������У�������ABC��A1B1C1�IJ���ABB1A1��Բ��������棬C��Բ������Բ���ϲ���A��B�غϵ�һ���㣮 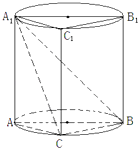
������Բ����������������Σ�����C�ǻ�AB���е�ʱ��������ֱ��A1C��AB1�����ɽǵĴ�С��
������C�ǻ�AB���е�ʱ��������A1��BCC1B1��Բ��������ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����˫����C�� ![]() ��F1 �� F2Ϊ�������������㣮
��F1 �� F2Ϊ�������������㣮
��1����OΪ����ԭ�㣬MΪ˫����C��֧������һ�㣬�� ![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2��������P��˫����C����������F1 �� F2�ľ���֮��Ϊ��ֵ����cos��F1PF2����СֵΪ ![]() ����P�Ĺ켣���̣�
����P�Ĺ켣���̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ԲC�� ![]() ����M��2��0�������ҽ���ΪF��1��0������F��ֱ��l����ԲC�ཻ��A��B���㣮���P��4��3������PA��PB��б�ʷֱ�Ϊk1��k2 ��
����M��2��0�������ҽ���ΪF��1��0������F��ֱ��l����ԲC�ཻ��A��B���㣮���P��4��3������PA��PB��б�ʷֱ�Ϊk1��k2 �� 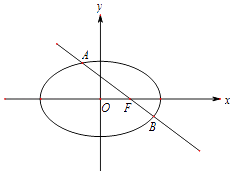
��1������ԲC�ķ��̣�
��2�����ֱ��l��б�ʵ��ک�1�����k1k2��ֵ��
��3��̽��k1+k2�Ƿ�Ϊ��ֵ������ǣ�����ö�ֵ��������ǣ����k1+k2��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ABC��A1B1C1�ĵ�������������Σ�����ڹ���A��ƽ�棨 �� 
A.��ֱ��BC��ֱ��A1B1��ƽ��
B.��ֱ��BC��ֱ��A1B1����ֱ
C.��ֱ��BCƽ����ֱ��A1B1��ֱ
D.��ֱ��BC��ֱ��A1B1���ɽ����
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com