
分析 (Ⅰ)令a=0,b=0得到f(0)[f(0)-1]=0,从而求出f(0);
(Ⅱ)令a=0,b=x得到以f(-x)=f(x),进而得出f(x)为偶函数;
(Ⅲ)令a=x,b=m得到f(x+2m)=-f(x),即可得出T=4m.
解答 解:(Ⅰ)令a=b=0,代入f(a+b)+f(a-b)=2f(a)•f(b)得,
f(0)+f(0)=2f(0)•f(0),
即f(0)[f(0)-1]=0,
因为f(0)≠0,所以f(0)=1;
(Ⅱ)令a=0,b=x,代入f(a+b)+f(a-b)=2f(a)•f(b)得,
f(x)+f(-x)=2f(0)•f(x)=2f(x),
所以f(-x)=f(x),
因此,函数f(x)为偶函数;
(Ⅲ)令a=x,b=m,代入f(a+b)+f(a-b)=2f(a)•f(b)得,
f(x+m)+f(x-m)=2f(x)•f(m)=0,
∵f(m)=0,∴f(x+m)=-f(x-m),
所以,f(x+2m)=-f(x),
所以,f(x+4m)=-f(x+2m)=f(x),
即f(x+4m)=f(x),
所以满足f(x+T)=f(x)的一个T值为4m.
点评 本题主要考查了抽象函数值的求解,函数奇偶性的判断与证明,以及抽象哈数周期的确定,属于中档题.


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{7}$ | B. | 2$\sqrt{3}$ | C. | 4 | D. | 3$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 现在阳台种菜成为部分人的爱好,如图所示,一块种菜的小菜地一面靠墙(墙长度为1.2米),另外三面由总长为2米的栅栏围成,设宽为x米.面积为y平方米.
现在阳台种菜成为部分人的爱好,如图所示,一块种菜的小菜地一面靠墙(墙长度为1.2米),另外三面由总长为2米的栅栏围成,设宽为x米.面积为y平方米.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
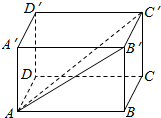 如图,长方体ABCD-A′B′C′D′中,化简下列各式,并在图中标出化简得到的向量:
如图,长方体ABCD-A′B′C′D′中,化简下列各式,并在图中标出化简得到的向量:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com