
【题目】有一名高二学生盼望2020年进入某名牌大学学习,假设该名牌大学有以下条件之一均可录取:①2020年2月通过考试进入国家数学奥赛集训队(集训队从2019年10月省数学竞赛一等奖中选拔);②2020年3月自主招生考试通过并且达到2020年6月高考重点分数线,③2020年6月高考达到该校录取分数线(该校录取分数线高于重点线),该学生具备参加省数学竞赛、自主招生和高考的资格且估计自己通过各种考试的概率如下表
省数学竞赛一等奖 | 自主招生通过 | 高考达重点线 | 高考达该校分数线 |
0.5 | 0.6 | 0.9 | 0.7 |
若该学生数学竞赛获省一等奖,则该学生估计进入国家集训队的概率是0.2.若进入国家集训队,则提前录取,若未被录取,则再按②、③顺序依次录取:前面已经被录取后,不得参加后面的考试或录取.(注:自主招生考试通过且高考达重点线才能录取)
(1)求该学生参加自主招生考试的概率;
(2)求该学生参加考试的次数![]() 的分布列及数学期望;
的分布列及数学期望;
科目:高中数学 来源: 题型:
【题目】已知函数![]()
![]() 相邻两对称轴间的距离为
相邻两对称轴间的距离为![]() ,若将
,若将![]() 的图象先向左平移
的图象先向左平移![]() 个单位,再向下平移1个单位,所得的函数
个单位,再向下平移1个单位,所得的函数![]() 为奇函数.
为奇函数.
(1)求![]() 的解析式,并求
的解析式,并求![]() 的对称中心;
的对称中心;
(2)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有两个不相等的实根,求实数
上有两个不相等的实根,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥![]() 底面的3个顶点
底面的3个顶点![]() 在球
在球![]() 的同一个大圆上,且
的同一个大圆上,且![]() 为正三角形,
为正三角形,![]() 为该球面上的点,若三棱锥
为该球面上的点,若三棱锥![]() 体积的最大值为
体积的最大值为![]() ,则球
,则球![]() 的表面积为( )
的表面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),曲线
),曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)设曲线![]() 与曲线
与曲线![]() 的交点分别为
的交点分别为![]() ,求
,求![]() 的最大值及此时直线
的最大值及此时直线![]() 的倾斜角.
的倾斜角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某沿海地区的海岸线为一段圆弧![]() ,对应的圆心角
,对应的圆心角![]() ,该地区为打击走私,在海岸线外侧
,该地区为打击走私,在海岸线外侧![]() 海里内的海域
海里内的海域![]() 对不明船只进行识别查证(如图:其中海域与陆地近似看作在同一平面内),在圆弧的两端点
对不明船只进行识别查证(如图:其中海域与陆地近似看作在同一平面内),在圆弧的两端点![]() 、
、![]() 分别建有监测站,
分别建有监测站,![]() 与
与![]() 之间的直线距离为
之间的直线距离为![]() 海里.
海里.

(1)求海域![]() 的面积;
的面积;
(2)现海上![]() 点处有一艘不明船只,在
点处有一艘不明船只,在![]() 点测得其距
点测得其距![]() 点
点![]() 海里,在
海里,在![]() 点测得其距
点测得其距![]() 点
点![]() 海里.判断这艘不明船只是否进入了海域
海里.判断这艘不明船只是否进入了海域![]() ?请说明理由.
?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】砂糖橘是柑橘类的名优品种,因其味甜如砂糖故名.某果农选取一片山地种植砂糖橘,收获时,该果农随机选取果树20株作为样本测量它们每一株的果实产量(单位:kg),获得的所有数据按照区间(40,45],(45,50],(50,55],(55,60]进行分组,得到频率分布直方图如图所示.已知样本中产量在区间(45,50]上的果树株数是产量在区间(50,60]上的果树株数的![]() 倍.
倍.
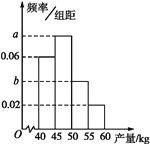
(1)求a,b的值;
(2)从样本中产量在区间(50,60]上的果树里随机抽取两株,求产量在区间(55,60]上的果树至少有一株被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分14分)围建一个面积为![]() 的矩形场地,要求矩形场地的一面利用旧墙(利用的旧墙需维修,可供利用的旧墙足够长),其他三面围墙要新建,在旧墙对面的新墙上要留一个宽
的矩形场地,要求矩形场地的一面利用旧墙(利用的旧墙需维修,可供利用的旧墙足够长),其他三面围墙要新建,在旧墙对面的新墙上要留一个宽![]() 的进出口,如图2所示.已知旧墙的维修费用为
的进出口,如图2所示.已知旧墙的维修费用为![]() ,新墙的造价为
,新墙的造价为![]() .设利用旧墙的长度为
.设利用旧墙的长度为![]() (单位:
(单位:![]() ),修建此矩形场地围墙的总费用为
),修建此矩形场地围墙的总费用为![]() (单位:元).
(单位:元).
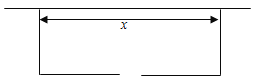
(1)将![]() 表示为
表示为![]() 的函数,并写出此函数的定义域;
的函数,并写出此函数的定义域;
(2)若要求用于维修旧墙的费用不得超过修建此矩形场地围墙的总费用的15%,试确定![]() ,使修建此矩形场地围墙的总费用最小,并求出最小总费用.
,使修建此矩形场地围墙的总费用最小,并求出最小总费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com