
【题目】(本小题共14分)如图,在三棱锥![]() 中,
中, ![]() 底面
底面
![]() ,点
,点![]() ,
, ![]() 分别在棱
分别在棱![]() 上,且
上,且![]() (Ⅰ)求证:
(Ⅰ)求证: ![]() 平面
平面![]() ;(Ⅱ)当
;(Ⅱ)当![]() 为
为![]() 的中点时,求
的中点时,求![]() 与平面
与平面![]() 所成的角的大小;(Ⅲ)是否存在点
所成的角的大小;(Ⅲ)是否存在点![]() 使得二面角
使得二面角![]() 为直二面角?并说明理由.
为直二面角?并说明理由.
【答案】(Ⅱ)![]() .
.
【解析】【解法1】本题主要考查直线和平面垂直、直线与平面所成的角、二面角等基础知识,考查空间想象能力、运算能力和推理论证能力.
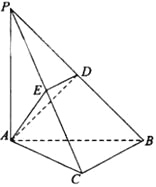 (Ⅰ)∵PA⊥底面ABC,∴PA⊥BC.
(Ⅰ)∵PA⊥底面ABC,∴PA⊥BC.
又![]() ,∴AC⊥BC.∴BC⊥平面PAC.
,∴AC⊥BC.∴BC⊥平面PAC.
(Ⅱ)∵D为PB的中点,DE//BC,
∴![]() ,又由(Ⅰ)知,BC⊥平面PAC,
,又由(Ⅰ)知,BC⊥平面PAC,
∴DE⊥平面PAC,垂足为点E.
∴∠DAE是AD与平面PAC所成的角,∵PA⊥底面ABC,
∴PA⊥AB,又PA=AB,∴△ABP为等腰直角三角形,
∴![]() ,∴在Rt△ABC中,
,∴在Rt△ABC中, ![]() ,∴
,∴![]() .∴在Rt△ADE中,
.∴在Rt△ADE中, ![]() ,∴
,∴![]() 与平面
与平面![]() 所成的角的大小
所成的角的大小![]() .
.
(Ⅲ)∵DE//BC,又由(Ⅰ)知,BC⊥平面PAC,∴DE⊥平面PAC,又∵AE![]() 平面PAC,PE
平面PAC,PE![]() 平面PAC,∴DE⊥AE,DE⊥PE,∴∠AEP为二面角
平面PAC,∴DE⊥AE,DE⊥PE,∴∠AEP为二面角![]() 的平面角,∵PA⊥底面ABC,∴PA⊥AC,∴
的平面角,∵PA⊥底面ABC,∴PA⊥AC,∴![]() .∴在棱PC上存在一点E,使得AE⊥PC,这时
.∴在棱PC上存在一点E,使得AE⊥PC,这时![]() ,故存在点E使得二面角
,故存在点E使得二面角![]() 是直二面角.
是直二面角.
【解法2】如图,以A为原煤点建立空间直角坐标系![]() ,设
,设![]() ,由已知可得
,由已知可得
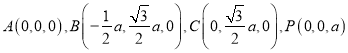 .
.
(Ⅰ)∵![]() ,∴
,∴![]() ,∴BC⊥AP.
,∴BC⊥AP.
又∵![]() ,∴BC⊥AC,∴BC⊥平面PAC.
,∴BC⊥AC,∴BC⊥平面PAC.
(Ⅱ)∵D为PB的中点,DE//BC,∴E为PC的中点,
∴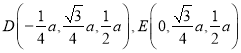 ,∴又由(Ⅰ)知,BC⊥平面PAC,∴∴DE⊥平面PAC,垂足为点E.∴∠DAE是AD与平面PAC所成的角,∵
,∴又由(Ⅰ)知,BC⊥平面PAC,∴∴DE⊥平面PAC,垂足为点E.∴∠DAE是AD与平面PAC所成的角,∵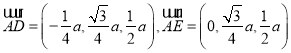 ,
,
∴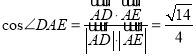 .∴
.∴![]() 与平面
与平面![]() 所成的角的大小
所成的角的大小![]() .
.
(Ⅲ)同解法1.


科目:高中数学 来源: 题型:
【题目】已知极坐标系的极点为直角坐标系xOy的原点,极轴为x轴的正半轴,两种坐标系中的长度单位相同![]() 直线
直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线C的参数方程为
,曲线C的参数方程为![]() 为参数
为参数![]() ,设直线l与曲线C交于A,B两点.
,设直线l与曲线C交于A,B两点.
![]() 写出直线
写出直线![]() 的普通方程与曲线C的直角坐标方程;
的普通方程与曲线C的直角坐标方程;
![]() 已知点P在曲线C上运动,求点P到直线
已知点P在曲线C上运动,求点P到直线![]() 距离的最大值.
距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是2017年第一季度中国某五省![]() 情况图,则下列陈述正确的是( )
情况图,则下列陈述正确的是( )
①2017年第一季度 ![]() 总量高于4000亿元的省份共有3个;
总量高于4000亿元的省份共有3个;
②与去年同期相比,2017年第一季度五个省的![]() 总量均实现了增长;
总量均实现了增长;
③去年同期的![]() 总量前三位依次是
总量前三位依次是![]() 省、
省、![]() 省、
省、![]() 省;
省;
④2016年同期![]() 省的
省的![]() 总量居于第四位.
总量居于第四位.
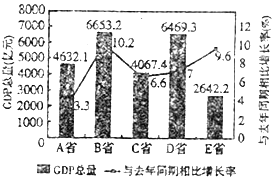
A. ①② B. ②③④ C. ②④ D. ①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高中生调查了当地某小区的50户居民由于台风造成的经济损失,将收集的数据分成![]() 三组,并作出如下频率分布直方图:
三组,并作出如下频率分布直方图:

(1)在直方图的经济损失分组中,以各组的区间中点值代表该组的各个值,并以经济损失落入该区间的频率作为经济损失取该区间中点值的概率(例如:经济损失![]() 则取
则取![]() ,且
,且![]() 的概率等于经济损失落入
的概率等于经济损失落入![]() 的频率)。现从当地的居民中随机抽出2户进行捐款援助,设抽出的2户的经济损失的和为
的频率)。现从当地的居民中随机抽出2户进行捐款援助,设抽出的2户的经济损失的和为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
(2)台风后居委会号召小区居民为台风重灾区捐款,此高中生调查的50户居民捐款情况如下表,在表格空白处填写正确数字,并说明是否有95%以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关?
经济损失不超过4000元 | 经济损失超过4000元 | 合计 | |
捐款超过500元 | 30 | ||
捐款不超过500元 | 6 | ||
合计 |
附:临界值表参考公式:  .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的焦距为2,左右焦点分别为
的焦距为2,左右焦点分别为![]() ,
,![]() ,以原点O为圆心,以椭圆C的半短轴长为半径的圆与直线
,以原点O为圆心,以椭圆C的半短轴长为半径的圆与直线![]() 相切.
相切.
![]() Ⅰ
Ⅰ![]() 求椭圆C的方程;
求椭圆C的方程;
![]() Ⅱ
Ⅱ![]() 设不过原点的直线l:
设不过原点的直线l:![]() 与椭圆C交于A,B两点.
与椭圆C交于A,B两点.
![]() 若直线
若直线![]() 与
与![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,且
,且![]() ,求证:直线l过定点,并求出该定点的坐标;
,求证:直线l过定点,并求出该定点的坐标;
![]() 若直线l的斜率是直线OA,OB斜率的等比中项,求
若直线l的斜率是直线OA,OB斜率的等比中项,求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]()
![]() 的左右焦点分别为的
的左右焦点分别为的![]() 、
、![]() ,离心率为
,离心率为![]() ;过抛物线
;过抛物线![]() 焦点
焦点![]() 的直线交抛物线于
的直线交抛物线于![]() 、
、![]() 两点,当
两点,当![]() 时,
时, ![]() 点在
点在![]() 轴上的射影为
轴上的射影为![]() 。连结
。连结![]() 并延长分别交
并延长分别交![]() 于
于![]() 、
、![]() 两点,连接
两点,连接![]() ;
; ![]() 与
与![]() 的面积分别记为
的面积分别记为![]() ,
, ![]() ,设
,设![]() .
.
(Ⅰ)求椭圆![]() 和抛物线
和抛物线![]() 的方程;
的方程;
(Ⅱ)求![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解学生对正在进行的一项教学改革的态度,从500名高一学生和400名高二学生中按分层抽样的方式抽取了45名学生进行问卷调查,结果可以分成以下三类:支持、反对、无所谓,调查结果统计如下:
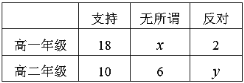
(1)(i)求出表中的![]() 的值;
的值;
(ii)从反对的同学中随机选取2人进一步了解情况,求恰好高一、高二各1人的概率;
(2)根据表格统计的数据,完成下面的![]() 的列联表,并判断是否有90%的把握认为持支持与就读年级有关.(不支持包括无所谓和反对)
的列联表,并判断是否有90%的把握认为持支持与就读年级有关.(不支持包括无所谓和反对)
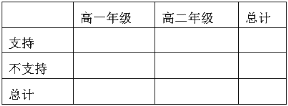
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com