
 (其中A>0,
(其中A>0, )的图象如图所示,为了得到
)的图象如图所示,为了得到 的图象,则只需将g(x)=sin2x的图象
的图象,则只需将g(x)=sin2x的图象
A.向右平移 个长度单位 个长度单位 |
B.向左平移 个长度单位 个长度单位 |
C.向右平移 个长度单位 个长度单位 |
D.向左平移 个长度单位 个长度单位 |
 )的图象,过(
)的图象,过( ,0)点,(
,0)点,(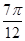 ,-1)点,易得:A=1,T=4(
,-1)点,易得:A=1,T=4(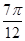 -
- )=π,即ω=2,即f(x)=sin(2x+φ),,
)=π,即ω=2,即f(x)=sin(2x+φ),,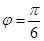 故可知向左平移
故可知向左平移 个长度单位,选B.
个长度单位,选B.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com