练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数设表示p、q中的较大值，表示p、q中的较小值）记的最小值为A，的最大值为B，则A-B＝

    A. 16 B. -16 C. a2-2a-16 D. a2+2a-1

    【答案】B

    【解析】

    在同一坐标系中画出f（x）与g（x）的图象，由图象及H1（x）的定义知H1（x）的最小值是f（a+2），H2（x）的最大值为g（a﹣2），进而可得答案．

    f（x）＝g（x），

    即x2﹣2（a+2）x+a2＝﹣x2+2（a﹣2）x﹣a2+8，

    即x2﹣2ax+a2﹣4＝0，

    解得x＝a+2或x＝a﹣2．

    f（x）与g（x）的图象如图．

    由图象及H1（x）的定义知H1（x）的最小值是f（a+2），

    H2（x）的最大值为g（a﹣2），

    A﹣B＝f（a+2）﹣g（a﹣2）

    ＝（a+2）2﹣2（a+2）2+a2+（a﹣2）2﹣2（a﹣2）2+a2﹣8＝﹣16．

    故答案为：B

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）求在处的切线方程;

    （2）若时,恒成立，求实数的取值范围；

    （3）求证：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知定义在R上的函数满足以下三个条件：①对于任意的，都有；②对于任意的都有③函数的图象关于y轴对称，则下列结论中正确的是( )

    A. B.

    C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知曲线C1：y=cos x，C2：y=sin (2x+)，则下面结论正确的是( )

    A. 把C1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移个单位长度，得到曲线C2

    B. 把C1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移个单位长度，得到曲线C2

    C. 把C1上各点的横坐标缩短到原来的倍，纵坐标不变，再把得到的曲线向右平移个单位长度，得到曲线C2

    D. 把C1上各点的横坐标缩短到原来的倍，纵坐标不变，再把得到的曲线向左平移个单位长度，得到曲线C2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆C经过点和，且圆心C在直线上.

    （1）求C圆的方程；

    （2）直线l过圆C外一点，且直线l与圆C只有一个公共点，求直线l的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知向量，，函数满足，且在区间上单调，又不等式对一切恒成立.

    （1）求函数的解析式；

    （2）若函数在区间的零点为，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，曲线的参数方程为（， 为参数），以坐标原点为极点， 轴正半轴为极轴建立极坐标系，直线的极坐标方程为，若直线与曲线相切；

    （1）求曲线的极坐标方程；

    （2）在曲线上取两点， 与原点构成，且满足，求面积的最大值.

    【答案】（1）；（2）

    【解析】试题分析：（1）利用极坐标与直角坐标的互化公式可得直线的直角坐标方程为，

    ，消去参数可知曲线是圆心为，半径为的圆，由直线与曲线相切，可得： ；则曲线C的方程为， 再次利用极坐标与直角坐标的互化公式可得

    可得曲线C的极坐标方程.

    (2)由（1）不妨设M（），，（），

    ，

    ，

    由此可求面积的最大值.

    试题解析：（1）由题意可知直线的直角坐标方程为，

    曲线是圆心为，半径为的圆，直线与曲线相切，可得： ；可知曲线C的方程为，

    所以曲线C的极坐标方程为，

    即.

    (2)由（1）不妨设M（），，（），

    ，

    ，

    当 时， ，

    所以△MON面积的最大值为.

    【题型】解答题
    【结束】
    23

    【题目】已知函数的定义域为；

    （1）求实数的取值范围；

    （2）设实数为的最大值，若实数， ， 满足，求的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

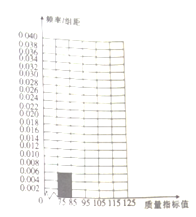
    【题目】某种产品的质量以其质量指标值衡量，质量指标值越大表明质量越好，现用一种新配方做试验，生产了100件这种产品，并测量了每件产品的质量指标值，得到下面试验结果：

    质量指标值

    频数

    6

    26

    38

    22

    8

    （1）将答题卡上列出的这些数据的频率分布表填写完整，并补齐频率分布直方图；

    （2）估计这种产品质量指标值的平均值（同一组中的数据用该组区间的中点值作代表）与中位数（结果精确到0.1）.

    质量指标值分组

    频数

    频率

    6

    0.06

    合计

    100

    1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆：和点，， ，.

    (1)若点是圆上任意一点，求；

    (2)过圆 上任意一点 与点的直线，交圆于另一点,连接，，求证：.

    查看答案和解析>>

    同步练习册答案