
 ,
, ,函数f(x)=
,函数f(x)=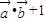 .
.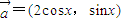 ,
, ,函数f(x)=
,函数f(x)=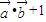 .我们根据向量数量积的运算公式及辅助角公式易将函数的解析式化为正弦型函数,根据正弦型函数的性质得到函数f(x)的单调递增区间.
.我们根据向量数量积的运算公式及辅助角公式易将函数的解析式化为正弦型函数,根据正弦型函数的性质得到函数f(x)的单调递增区间.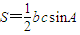 ,即可得到△ABC面积S的最大值.
,即可得到△ABC面积S的最大值.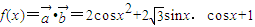
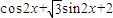 ------(2分)
------(2分) --------(3分)
--------(3分)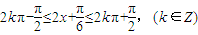 --------(5分)
--------(5分)
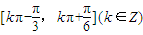 -------(7分)
-------(7分)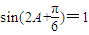 0<A<π,
0<A<π,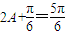 ,∴
,∴ -----------(9分)
-----------(9分) ∴S的最大值为
∴S的最大值为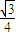 ---------(14分)
---------(14分)

科目:高中数学 来源:2010-2011学年浙江省温州市十校联合体高三(上)期末数学试卷(理科)(解析版) 题型:解答题
 ,
,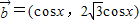 ,函数f(x)=
,函数f(x)=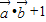 .
.查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省杭州市高一(上)期末数学试卷(解析版) 题型:解答题
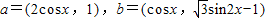 ,设函数f(x)=a•b,其中x∈R.
,设函数f(x)=a•b,其中x∈R.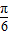 个单位得到g(x)的图象,求g(x)的解析式.
个单位得到g(x)的图象,求g(x)的解析式.查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省苏州市高一(上)期末数学复习试卷3(解析版) 题型:解答题
 ,
,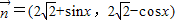 ,函数f(x)=
,函数f(x)= ,x∈R.
,x∈R.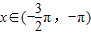 ,且f(x)=1,求
,且f(x)=1,求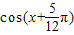 的值.
的值.查看答案和解析>>
科目:高中数学 来源:2011年浙江省杭州市萧山区高考数学模拟试卷02(文科)(解析版) 题型:解答题
 ,
, ,函数f(x)=
,函数f(x)= .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com