
【题目】在四棱锥P—ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2.以BD的中点O为球心,BD为直径的球面交PD于点M.
(1)求证:平面ABM⊥平面PCD;
(2)求直线PC与平面ABM所成的角的正切值.
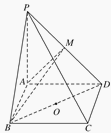
【答案】(1)见解析;(2)2![]()
【解析】
(1)先证明PD⊥平面ABM,再证明平面ABM⊥平面PCD.(2) 设平面ABM与PC交于点N,连接BN,MN,再证明∠PNM就是PC与平面ABM所成的角,再解三角形求得直线PC与平面ABM所成的角的正切值.
(1)证明:依题设,M在以BD为直径的球面上,则BM⊥PD
因为PA⊥平面ABCD,则PA⊥AB,又AB⊥AD,![]() 所以AB⊥平面PAD,
所以AB⊥平面PAD,![]() 则AB⊥PD,
则AB⊥PD,
![]() 因此有PD⊥平面ABM,
因此有PD⊥平面ABM,
![]() 所以平面ABM⊥平面PCD.
所以平面ABM⊥平面PCD.
(2)设平面ABM与PC交于点N,连接BN,MN,
因为AB∥CD,所以AB∥平面PCD,则AB∥MN∥CD.
由(1)知,PD⊥平面ABM,则MN是PN在平面ABM上的射影,
所以∠PNM就是PC与平面ABM所成的角,
且∠PNM=∠PCD,tan∠PNM=tan∠PCD=![]() =2
=2![]() .
.
即所求角的正切值为2![]() .
.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】如图,设a,b,c,d>0,且不等于1,y=ax , y=bx , y=cx , y=dx在同一坐标系中的图象如图,则a,b,c,d的大小顺序( ) 
A.a<b<c<d
B.a<b<d<c
C.b<a<d<c
D.b<a<c<d
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:x∈R,x2+1>m;命题q:指数函数f(x)=(3﹣m)x是增函数.若“p∧q”为假命题且“p∨q”为真命题,则实数m的取值范围为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数exf(x)(e≈2.71828…是自然对数的底数)在f(x)的定义域上单调递增,则称函数f(x)具有M性质.下列函数中所有具有M性质的函数的序号为 .
①f(x)=2﹣x②f(x)=3﹣x③f(x)=x3④f(x)=x2+2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,椭圆E: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,焦距为2.(14分)
,焦距为2.(14分)
(Ⅰ)求椭圆E的方程.
(Ⅱ)如图,该直线l:y=k1x﹣ ![]() 交椭圆E于A,B两点,C是椭圆E上的一点,直线OC的斜率为k2 , 且看k1k2=
交椭圆E于A,B两点,C是椭圆E上的一点,直线OC的斜率为k2 , 且看k1k2= ![]() ,M是线段OC延长线上一点,且|MC|:|AB|=2:3,⊙M的半径为|MC|,OS,OT是⊙M的两条切线,切点分别为S,T,求∠SOT的最大值,并求取得最大值时直线l的斜率.
,M是线段OC延长线上一点,且|MC|:|AB|=2:3,⊙M的半径为|MC|,OS,OT是⊙M的两条切线,切点分别为S,T,求∠SOT的最大值,并求取得最大值时直线l的斜率.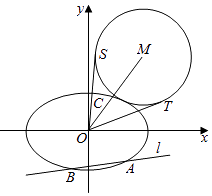
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列{an}的前n项和为Sn , ![]() ,若
,若 ![]() ,且S11=143,数列{bn}的前n项和为Tn , 且满足
,且S11=143,数列{bn}的前n项和为Tn , 且满足 ![]() .
.
(1)求数列{an}的通项公式及数列 ![]() 的前n项和Mn
的前n项和Mn
(2)是否存在非零实数λ,使得数列{bn}为等比数列?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班级数学兴趣小组为了研究人的脚的大小与身高的关系,随机抽测了20位同学,得到如下数据:
序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
身高x(厘米) | 192 | 164 | 172 | 177 | 176 | 159 | 171 | 166 | 182 | 166 |
脚长y(码) | 48 | 38 | 40 | 43 | 44 | 37 | 40 | 39 | 46 | 39 |
序号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
身高x(厘米) | 169 | 178 | 167 | 174 | 168 | 179 | 165 | 170 | 162 | 170 |
脚长y(码) | 43 | 41 | 40 | 43 | 40 | 44 | 38 | 42 | 39 | 41 |
(Ⅰ)请根据“序号为5的倍数”的几组数据,求出y关于x的线性回归方程
(Ⅱ)若“身高大于175厘米”为“高个”,“身高小于等于175厘米”的为“非高个”;“脚长大于42码”为“大码”,“脚长小于等于42码”的为“非大码”.请根据上表数据完成2×2列联表:并根据列联表中数据说明能有多大的可靠性认为脚的大小与身高之间有关系?
(Ⅲ)若按下面的方法从这20人中抽取1人来核查测量数据的误差:将一个标有1,2,3,4,5,6的正六面体骰子连续投掷两次,记朝上的两个数字的乘积为被抽取人的序号,求:抽到“无效序号(超过20号)”的概率.
附表及公式:
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
K2= ![]()
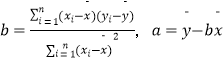 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com