
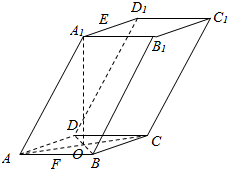
 如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD为菱形,AB=1,∠DAB=60°,AA1=$\sqrt{3}$,BD中点为O,A1O⊥平面ABCD,E、F分别为A1D1,AB的中点.
如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD为菱形,AB=1,∠DAB=60°,AA1=$\sqrt{3}$,BD中点为O,A1O⊥平面ABCD,E、F分别为A1D1,AB的中点.分析 (1)取A1B1的中点G,由线面平行证面面平行,再由面面平行得线面平行;
(2)利用等积法把三棱锥A1-BDC1的体积转化为三棱锥C1-A1BD的体积求解.
解答 (1)证明:取A1B1的中点G,连接EG、GF,则EG∥D1B1,∴EG∥平面BB1D1D,
GF∥BB1,∴GF∥平面BB1D1D,
又EG∩GF=G,∴平面EGF∥平面BB1D1D1,
则EF∥平面BB1D1D1;
(2)解:∵AB=1,∠DAB=60°,∴AO=$\frac{\sqrt{3}}{2}$,
在Rt△A1OA中,又AA1=$\sqrt{3}$,∴∠A1AO=60°,
则A1C1⊥平面A1BD,∴A1C1为三棱锥C1-A1BD的高,等于AC=$\sqrt{3}$.
∴${V}_{{A}_{1}-BD{C}_{1}}={V}_{{C}_{1}-{A}_{1}BD}=\frac{1}{3}•\frac{1}{2}BD•{A}_{1}O{•A}_{1}{C}_{1}$=$\frac{1}{3}×\frac{1}{2}×1×\frac{1}{2}×\sqrt{3}=\frac{\sqrt{3}}{12}$.
点评 本题给出底面为菱形的四棱柱,证明直线与平面平行并探求了平面与平面成直角的问题,着重考查了线面平行的判定,以及利用等积法转化求棱锥的体积等知识,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | U=A∪B | B. | U=∁UA∪B | C. | U=A∪∁UB | D. | U=∁UA∪∁UB |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(α+$\frac{5π}{6}$)>f(α+$\frac{π}{12}$) | B. | f(α+$\frac{5π}{6}$)<f(α+$\frac{π}{12}$) | C. | f(α+$\frac{5π}{6}$)=f(α+$\frac{π}{12}$) | D. | 大小与α,φ有关 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 地区 | A | B | C |
| 数量 | 50 | 150 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 一定等于0 | B. | 一定小于0 | C. | 一定大于0 | D. | 符号不能确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com