
【题目】前段时间,某机构调查人们对屯商平台“618”活动的认可度(分为:强烈和一般两类),随机抽取了100人统计得到2×2列联表的部分数据如表:
一般 | 强烈 | 合计 | |
男 | 45 | ||
女 | 10 | ||
合计 | 75 | 100 |
(1)补全2×2列联表中的数据;
(2)判断能否有95%的把握认为人们的认可度是否为“强烈”与性别有关?
参考公式及数据: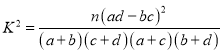
| 0.05 | 0.025 | 0.010 | 0.005 |
| 3.841 | 5.024 | 6.635 | 7.879 |
科目:高中数学 来源: 题型:
【题目】某地随着经济的发展,居民收入逐年增长该地一建设银行统计连续五年的储蓄存款(年底余额)得到下表:
年份x | 2014 | 2015 | 2016 | 2017 | 2018 |
储蓄存款y(千亿元) | 5 | 6 | 7 | 8 | 10 |
为便于计算,工作人员将上表的数据进行了处理(令![]()
![]() ),得到下表:
),得到下表:
时间t | 1 | 2 | 3 | 4 | 5 |
储蓄存款z | 0 | 1 | 2 | 3 | 5 |
(1)求z关于t的线性回归方程;
(2)通过(1)中的方程,求出y关于x的回归方程;
(3)用所求回归方程预测到2020年年底,该地储蓄存款额可达多少?
附:线性回归方程![]() ,其中
,其中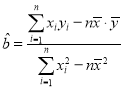 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 及圆
及圆![]() .
.
(1)若直线![]() 过点
过点![]() 且与圆心
且与圆心![]() 的距离为1,求直线
的距离为1,求直线![]() 的方程;
的方程;
(2)设过点![]() 的直线
的直线![]() 与圆
与圆![]() 交于
交于![]() 两点,当
两点,当![]() 时,求以线段
时,求以线段![]() 为直径的圆
为直径的圆![]() 的方程;
的方程;
(3)设直线![]() 与圆
与圆![]() 交于
交于![]() 两点,是否存在实数
两点,是否存在实数![]() ,使得过点
,使得过点![]() 的直线
的直线![]() 垂直平分弦
垂直平分弦![]() ?若存在,求出实数
?若存在,求出实数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】班级新年晚会设置抽奖环节.不透明纸箱中有大小相同的红球3个,黄球2个,且这5个球外别标有数字1、2、3、4、5.有如下两种方案可供选择:
方案一:一次性抽取两球,若颜色相同,则获得奖品;
方案二:依次有放回地抽取两球,若数字之和大于5,则获得奖品.
(1)写出按方案一抽奖的试验的所有基本事件;
(2)哪种方案获得奖品的可能性更大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,已知椭圆![]() 经过点
经过点![]() ,且其左右焦点的坐标分别是
,且其左右焦点的坐标分别是![]() ,
,![]() .
.
(1)求椭圆![]() 的离心率及标准方程;
的离心率及标准方程;
(2)设![]() 为动点,其中
为动点,其中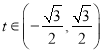 ,直线
,直线![]() 经过点
经过点![]() 且与椭圆
且与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,若
两点,若![]() 为
为![]() 的中点,是否存在定点
的中点,是否存在定点![]() ,使
,使![]() 恒成立?若存在,求点
恒成立?若存在,求点![]() 的坐标;若不存在,说明理由
的坐标;若不存在,说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在(0,+∞)上的增函数,且满足f(xy)=f(x)+f(y),f(2)=1.
(1)求f(8)的值;
(2)求不等式f(x)-f(x-2)>3的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P-ABCD中,ABCD为梯形,AB//CD,BC⊥AB,AB=2![]() ,BC=
,BC=![]() ,CD=PC=
,CD=PC=![]() 。
。
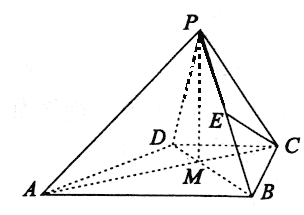
(I)点E在线段PB上,满足CE//平面PAD,求![]() 的值。
的值。
(II)已知AC与BD的交点为M,若PM=1,且平面PAC⊥平面ABCD,求二面角P-BC-M平面角的余弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某运动员射击一次所得环数![]() 的分布列如下:
的分布列如下:
| 8 | 9 | 10 |
| 0.4 | 0.4 | 0.2 |
现进行两次射击,且两次射击互不影响,以该运动员两次射击中最高环数作为他的成绩,记为![]() .
.
(1)求该运动员两次命中的环数相同的概率;
(2)求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com