
【题目】已知椭圆方程为 ![]() +y2=1,圆C:(x﹣1)2+y2=r2 .
+y2=1,圆C:(x﹣1)2+y2=r2 . 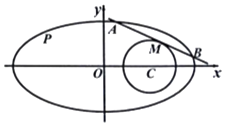
(Ⅰ)求椭圆上动点P与圆心C距离的最小值;
(Ⅱ)如图,直线l与椭圆相交于A、B两点,且与圆C相切于点M,若满足M为线段AB中点的直线l有4条,求半径r的取值范围.
【答案】解:(Ⅰ)设P(x,y),丨PC丨= ![]() =
= ![]() =
= ![]() ,
,
由﹣2≤x≤2,当x= ![]() 时,丨PC丨min=
时,丨PC丨min= ![]() ,
,
(Ⅱ)当直线AB斜率不存在时且与椭圆C相切时,M在x轴上,
故满足条件的直线有两条;
当直线AB斜率存在时,设A(x1,y1),B(x2,y2),M(x0,y0),
由 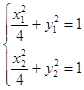 ,整理得:
,整理得: ![]() =﹣
=﹣ ![]() ×
× ![]() ,
,
则kAB=﹣ ![]() ,kMC=
,kMC= ![]() ,kMC×kAB=﹣1,
,kMC×kAB=﹣1,
则kMC×kAB=﹣ ![]() ×
× ![]() =﹣1,解得:x0=
=﹣1,解得:x0= ![]() ,
,
由M在椭圆内部,则 ![]() ,解得:y02<
,解得:y02< ![]() ,
,
由:r2=(x0﹣1)2+y02= ![]() +y02,
+y02,
∴ ![]() <r2<
<r2< ![]() ,解得:
,解得: ![]() <r<
<r< ![]() .
.
∴半径r的取值范围( ![]() ,
, ![]() )
)
【解析】(Ⅰ)利用两点之间的距离公式,根据x的取值范围,即可求得丨PC丨的最小值;(Ⅱ)利用点差法求得直线AB的斜率,根据kMC×kAB=﹣1,求得M点坐标,由 ![]() ,求得y02<
,求得y02< ![]() ,由圆的方程,即可求得半径r的取值范围.
,由圆的方程,即可求得半径r的取值范围.


科目:高中数学 来源: 题型:
【题目】以下排列的数是二项式系数在三角形中的几何排列,在我国南宋数学家杨辉1261年所著 的《详解九章算法》一书里就出现了.在欧洲,这个表叫做帕斯卡三角形,它出现要比杨辉迟393年. 那么,第2017行第2016个数是( )
A.2016
B.2017
C.2033136
D.2030112
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知离心率为 ![]() 的椭圆C:
的椭圆C: ![]() +
+ ![]() =1(a>b>0)过点P(﹣1,
=1(a>b>0)过点P(﹣1, ![]() ).
).
(1)求椭圆C的方程;
(2)直线AB:y=k(x+1)交椭圆C于A、B两点,交直线l:x=m于点M,设直线PA、PB、PM的斜率依次为k1、k2、k3 , 问是否存在实数t,使得k1+k2=tk3?若存在,求出实数t的值以及直线l的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)为R上的可导函数,且对x∈R,均有f(x)>f′(x),则有( )
A.e2016f(﹣2016)<f(0),f(2016)<e2016f(0)
B.e2016f(﹣2016)>f(0),f(2016)>e2016f(0)
C.e2016f(﹣2016)<f(0),f(2016)>e2016f(0)
D.e2016f(﹣2016)>f(0),f(2016)<e2016f(0)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)过点(
(a>b>0)过点( ![]() ,1),且焦距为2
,1),且焦距为2 ![]() .
.
(1)求椭圆C的方程;
(2)若直线l:y=k(x+1)(k>﹣2)与椭圆C相交于不同的两点A、B,线段AB的中点M到直线2x+y+t=0的距离为 ![]() ,求t(t>2)的取值范围.
,求t(t>2)的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知α∈[0,π),在直角坐标系xOy中,直线l1的参数方程为 ![]() (t为参数);在以坐标原点O为极点,x轴的正半轴为极轴的极坐标系中,直线l2的极坐标方程是ρcos(θ﹣α)=2sin(α+
(t为参数);在以坐标原点O为极点,x轴的正半轴为极轴的极坐标系中,直线l2的极坐标方程是ρcos(θ﹣α)=2sin(α+ ![]() ).
).
(Ⅰ)求证:l1⊥l2
(Ⅱ)设点A的极坐标为(2, ![]() ),P为直线l1 , l2的交点,求|OP||AP|的最大值.
),P为直线l1 , l2的交点,求|OP||AP|的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com