
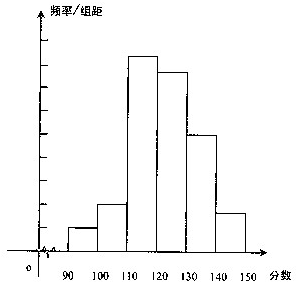
 某学校2012届高三高考前最后一次摸拟考试数学成绩统计整理后,画出频率分布直方图(如图),图中从左到右各小方形面积之比为(2:4:17:15:9:3,)其中成绩为100~110人数为28,则成绩为140~150的人数为
某学校2012届高三高考前最后一次摸拟考试数学成绩统计整理后,画出频率分布直方图(如图),图中从左到右各小方形面积之比为(2:4:17:15:9:3,)其中成绩为100~110人数为28,则成绩为140~150的人数为 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
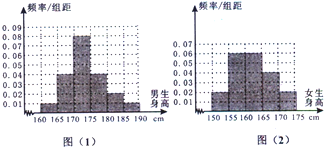 (2012•泉州模拟)某学校为调查高三年学生的身高情况,按随机抽样的方法抽取80名学生,得到男生身高情况的频率分布直方图(图(1)和女生身高情况的频率分布直方图(图(2)).已知图(1)中身高在170~175cm的男生人数有16人.
(2012•泉州模拟)某学校为调查高三年学生的身高情况,按随机抽样的方法抽取80名学生,得到男生身高情况的频率分布直方图(图(1)和女生身高情况的频率分布直方图(图(2)).已知图(1)中身高在170~175cm的男生人数有16人.| ≥170cm | <170cm | 总计 | |
| 男生身高 | |||
| 女生身高 | |||
| 总计 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2010•桂林二模)(注意:在试题卷上作答无效)
(2010•桂林二模)(注意:在试题卷上作答无效)查看答案和解析>>
科目:高中数学 来源: 题型:

| P(x2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
| ≥170cm | <170cm | 总计 | |
| 男生身高 | |||
| 女生身高 | |||
| 总计 |
| n(n11n22-n12n21)2 |
| n1+n2+n1+n2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com