
【题目】对于定义在![]() 上的函数
上的函数![]() ,若存在距离为
,若存在距离为![]() 的两条直线
的两条直线![]() 和
和![]() ,使得对任意
,使得对任意![]() 都有
都有![]() 恒成立,则称函数
恒成立,则称函数![]() 有一个宽度为
有一个宽度为![]() 的通道,给出下列函数:①
的通道,给出下列函数:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中在区间
.其中在区间![]() 上通道宽度可以为1的函数的个数是( )
上通道宽度可以为1的函数的个数是( )
A. 1 B. 2 C. 3 D. 4
科目:高中数学 来源: 题型:
【题目】设A是实数集,满足若a∈A,则![]() ∈A,a≠1,且1A.
∈A,a≠1,且1A.
(1)若2∈A,则集合A中至少还有几个元素?求出这几个元素.
(2)集合A中能否只含有一个元素?请说明理由.
(3)若a∈A,证明:1-![]() ∈A.
∈A.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义满足“如果a∈A,b∈A,那么a±b∈A,且ab∈A,且![]() ∈A(b≠0)”的集合A为“闭集”.试问数集N,Z,Q,R是否分别为“闭集”?若是,请说明理由;若不是,请举反例说明.
∈A(b≠0)”的集合A为“闭集”.试问数集N,Z,Q,R是否分别为“闭集”?若是,请说明理由;若不是,请举反例说明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的三个内角A、B、C所对的边分别是a、b、c,向量m=(cos B,cos C),n=(2a+c,b),且m⊥n.
(1)求角B的大小;
(2)若b=![]() ,求a+c的取值范围.
,求a+c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
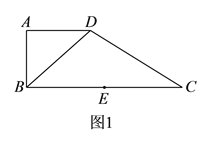
【题目】如图![]() ,在直角梯形
,在直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,点
,点![]() 是
是![]() 边的中点,将
边的中点,将![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() ,连接
,连接![]() ,
, ![]() ,
, ![]() ,得到如图
,得到如图![]() 所示的几何体.
所示的几何体.
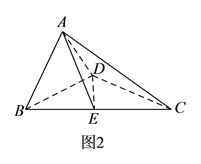
(Ⅰ)求证: ![]() 平面
平面![]() .
.
(Ⅱ)若![]() ,
, ![]() 与其在平面
与其在平面![]() 内的正投影所成角的正切值为
内的正投影所成角的正切值为![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4;坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点, ![]() 轴正半轴为极轴的极坐标中,曲线
轴正半轴为极轴的极坐标中,曲线![]() .
.
(Ⅰ)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程.
的直角坐标方程.
(Ⅱ)求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
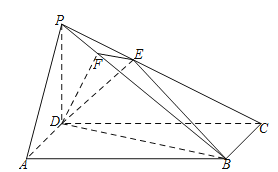
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是长方形,侧棱
是长方形,侧棱![]() 底面
底面![]() ,且
,且![]() ,过D作
,过D作![]() 于F,过F作
于F,过F作![]() 交 PC于E.
交 PC于E.
(Ⅰ)证明:![]() 平面PBC;
平面PBC;
(Ⅱ)求平面![]() 与平面
与平面![]() 所成二面角的余弦值.
所成二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车是城市慢行系统的一种模式创新,对于解决民众出行“最后一公里”的问题特别见效,由于停取方便、租用价格低廉,各色共享单车受到人们的热捧.某自行车厂为共享单车公司生产新样式的单车,已知生产新样式单车的固定成本为20000元,每生产一件新样式单车需要增加投入100元.根据初步测算,自行车厂的总收益(单位:元)满足分段函数![]() ,其中
,其中
![]() 是新样式单车的月产量(单位:件),利润
是新样式单车的月产量(单位:件),利润![]() 总收益
总收益![]() 总成本.
总成本.
(1)试将自行车厂的利润![]() 元表示为月产量
元表示为月产量![]() 的函数;
的函数;
(2)当月产量为多少件时自行车厂的利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com