
| A. | x2+y2=$\frac{1}{5}$ | B. | (x-1)2+y2=$\frac{2}{5}$ | C. | x2+y2=$\frac{4}{5}$ | D. | x2+y2=$\frac{3}{5}$ |
分析 由题意画出图形,求出原点到菱形边的距离得答案.
解答 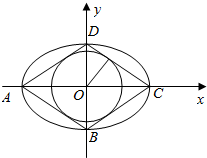 解:如图,
解:如图,
由$\frac{{x}^{2}}{4}$+y2=1,得C(2,0),D(0,1),
∴CD所在直线方程为$\frac{x}{2}+y=1$,即x+2y-2=0,
原点O到直线x+2y-2=0的距离为d=$\frac{|-2|}{\sqrt{5}}=\frac{2\sqrt{5}}{5}$,
即四边形ABCD的内切圆的半径为$\frac{2\sqrt{5}}{5}$.
∴四边形ABCD的内切圆方程是${x}^{2}+{y}^{2}=\frac{4}{5}$.
故选:C.
点评 本题考查椭圆的简单性质,考查数形结合的解题思想方法,是基础题.


科目:高中数学 来源: 题型:解答题
 如图,在平面直角坐标系xoy中,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为e=$\frac{\sqrt{3}}{2}$,过椭圆由焦点F作两条互相垂直的弦AB与CD.当直线AB斜率为0时,弦AB长4.
如图,在平面直角坐标系xoy中,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为e=$\frac{\sqrt{3}}{2}$,过椭圆由焦点F作两条互相垂直的弦AB与CD.当直线AB斜率为0时,弦AB长4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com