
分析 (Ⅰ)利用导数转化为求解最大值,最小值的差证明.
(Ⅱ)根据最大值为;f(-2)=$\frac{4}{{e}^{2}}$-b,f(x)的最小值为:-b,
分类当b<0时,当b=0时,当b=$\frac{4}{{e}^{2}}$时,当0<b<$\frac{4}{{e}^{2}}$时,当b>$\frac{4}{{e}^{2}}$时,判断即可.
解答 解:(Ⅰ)f(x)的定义域R,且f′(x)=x(x+2)ex,
令f′(x)=0则x1=0,或x2=-2,
f′(x)=x(x+2)ex,
| x | (-∞,-2) | -2 | (-2,0) |
| f′(x) | + | 0 | - |
| f(x) | 增函数 | 极大值 | 减函数 |
点评 本题考查了综合解决函数零点问题,利用导数解决单调性,最值,分类讨论的思想.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{4}$ | B. | $\frac{7}{5}$ | C. | $\frac{15}{4}$ | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 4 | C. | 5 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
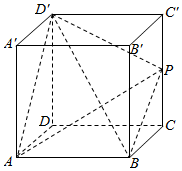 在棱长为4的正方体ABCD-A′B′C′D′中,点P在棱CC′上,且CC′=2CP.
在棱长为4的正方体ABCD-A′B′C′D′中,点P在棱CC′上,且CC′=2CP.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com