
【题目】在一次篮球定点投篮训练中,规定每人最多投3次,在![]() 处每投进一球得3分;在
处每投进一球得3分;在![]() 处每投进一球得2分,如果前两次得分之和超过3分就停止投篮;否则投第3次,某同学在
处每投进一球得2分,如果前两次得分之和超过3分就停止投篮;否则投第3次,某同学在![]() 处的抽中率
处的抽中率![]() ,在
,在![]() 处的抽中率为
处的抽中率为![]() ,该同学选择现在
,该同学选择现在![]() 处投第一球,以后都在
处投第一球,以后都在![]() 处投,且每次投篮都互不影响,用
处投,且每次投篮都互不影响,用![]() 表示该同学投篮训练结束后所得的总分,其分布列为:
表示该同学投篮训练结束后所得的总分,其分布列为:
| 0 | 2 | 3 | 4 | 5 |
| 0.03 |
|
|
|
|
(1)求![]() 的值;
的值;
(2)求随机变量![]() 的数学期望
的数学期望![]() ;
;
(3)试比较该同学选择上述方式投篮得分超过3分与选择都在![]() 处投篮得分超过3分的概率的大小.
处投篮得分超过3分的概率的大小.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)该同学选择上述方式投篮得分超过
;(3)该同学选择上述方式投篮得分超过![]() 分的概率大于选择都在
分的概率大于选择都在![]() 处投篮得分超过
处投篮得分超过![]() 分的概率.
分的概率.
【解析】
试题分析:(1)根据![]() ,解得
,解得![]() ;(2)根据相互独立事件概率计算公式,计算得
;(2)根据相互独立事件概率计算公式,计算得![]() ,由此计算得期望为
,由此计算得期望为![]() ;(3)用
;(3)用![]() 表示事件“该同学在
表示事件“该同学在![]() 处投第一球,以后都在
处投第一球,以后都在![]() 处投,得分超过
处投,得分超过![]() 分”,用
分”,用![]() 表示事件“该同学都在
表示事件“该同学都在![]() 处投,得分超过
处投,得分超过![]() 分”,计算得
分”,计算得![]() ,
,![]() .
.
试题解析:
(1)由题意可知,![]() 对应的事件为“三次投篮没有一次投中”,
对应的事件为“三次投篮没有一次投中”,
∴![]() ,
,
∵![]() ,解得
,解得![]() ;
;
(2)根据题意![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
∴![]() ,
,
(3)用![]() 表示事件“该同学在
表示事件“该同学在![]() 处投第一球,以后都在
处投第一球,以后都在![]() 处投,得分超过3分”,用
处投,得分超过3分”,用![]() 表示事件“该同学都在
表示事件“该同学都在![]() 处投,得分超过3分”,
处投,得分超过3分”,
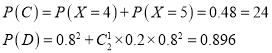 ,∴
,∴![]() ,
,
即该同学选择都在![]() 处投篮得分超过3分的概率的大于该同学在
处投篮得分超过3分的概率的大于该同学在![]() 处投第一球,以后都在
处投第一球,以后都在![]() 处投,得分超过3分的概率.
处投,得分超过3分的概率.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+bx(a≠0)的导函数f′(x)=-2x+7,数列{an}的前n项和为Sn,点Pn(n,Sn)(n∈N*)均在函数y=f(x)的图象上,求数列{an}的通项公式及Sn的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 的对称轴为
的对称轴为![]() ,
,![]() .
.
(1)求函数![]() 的最小值及取得最小值时
的最小值及取得最小值时![]() 的值;
的值;
(2)试确定![]() 的取值范围,使
的取值范围,使![]() 至少有一个实根;
至少有一个实根;
(3)当![]() 时,
时,![]() ,对任意
,对任意![]() 有
有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】网络购物已经被大多数人接受,随着时间的推移,网络购物的人越来越多,然而也有部分人对网络购物的质量和信誉产生怀疑。对此,某新闻媒体进行了调查,在所有参与调查的人中,持“支持”和“不支持”态度的人数如下表所示:
年龄 态度 | 支持 | 不支持 |
20岁以上50岁以下 | 800 | 200 |
50岁以 (含50岁) | 100 | 300 |
(1)在所有参与调查的人中,用分层抽样的方法抽取![]() 个人,已知从持“支持”态度的人中抽取了9人,求
个人,已知从持“支持”态度的人中抽取了9人,求![]() 的值;
的值;
(2)是否有99.9%的把握认为支持网络购物与年龄有关?
参考数据:
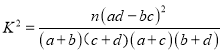 ,其中
,其中![]() ,
,
| 0.05 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是菱形,
是菱形,![]() ,侧面
,侧面![]() 是边长为2的等边三角形,点
是边长为2的等边三角形,点![]() 是
是![]() 的中点,且平面
的中点,且平面![]() 平面
平面![]() .
.
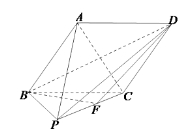
(I)求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(II)若点![]() 在线段
在线段![]() 上移动,是否存在点
上移动,是否存在点![]() 使平面
使平面![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ?若存在,指出点
?若存在,指出点![]() 的位置,否则说明理由.
的位置,否则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知随机变量X~N(μ,σ2),且其正态曲线在(-∞,80)上是增函数,在(80,+∞)上为减函数,且P(72≤X≤88)=0.682 6.
(1)求参数μ,σ的值;
(2)求P(64<X≤72).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某生态园将一三角形地块![]() 的一角
的一角![]() 开辟为水果园种植桃树,已知角
开辟为水果园种植桃树,已知角![]() 为
为![]() ,
,![]() 的长度均大于
的长度均大于![]() 米,现在边界
米,现在边界![]() 处建围墙,在
处建围墙,在![]() 处围竹篱笆.
处围竹篱笆.
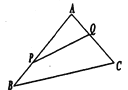
(1)若围墙![]() 总 长度为
总 长度为![]() 米,如何围可使得三角形地块
米,如何围可使得三角形地块![]() 的面积最大?
的面积最大?
(2)已知![]() 段围墙高
段围墙高![]() 米,
米,![]() 段围墙高
段围墙高![]() 米,造价均为每平方米
米,造价均为每平方米![]() 元.若围围墙用了
元.若围围墙用了![]() 元,问如何围可使竹篱笆用料最省?
元,问如何围可使竹篱笆用料最省?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com