
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)在极坐标系下,设曲线![]() 与射线
与射线![]() 和射线
和射线![]() 分别交于
分别交于![]() ,
,![]() 两点,求
两点,求![]() 的面积;
的面积;
(2)在直角坐标系下,直线![]() 的参数方程为
的参数方程为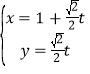 (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:
【题目】设点![]() 为圆
为圆![]() 上的动点,点
上的动点,点![]() 在
在![]() 轴上的投影为
轴上的投影为![]() ,动点
,动点![]() 满足
满足![]() ,动点
,动点![]() 的轨迹为
的轨迹为![]() .
.
(1)求![]() 的方程;
的方程;
(2)设![]() 与
与![]() 轴正半轴的交点为
轴正半轴的交点为![]() ,过点
,过点![]() 的直线
的直线![]() 的斜率为
的斜率为![]() ,
,![]() 与
与![]() 交于另一点为
交于另一点为![]() .若以点
.若以点![]() 为圆心,以线段
为圆心,以线段![]() 长为半径的圆与
长为半径的圆与![]() 有4个公共点,求
有4个公共点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知极坐标系的极点在平面直角坐标系的原点![]() 处,极轴与
处,极轴与![]() 轴的非负半轴重合,且长度单位相同,直线
轴的非负半轴重合,且长度单位相同,直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() (
(![]() 为参数).其中
为参数).其中![]() .
.
(1)试写出直线![]() 的直角坐标方程及曲线
的直角坐标方程及曲线![]() 的普通方程;
的普通方程;
(2)若点![]() 为曲线
为曲线![]() 上的动点,求点
上的动点,求点![]() 到直线
到直线![]() 距离的最大值.
距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() ,若椭圆
,若椭圆![]() :
:![]() ,则称椭圆
,则称椭圆![]() 与椭圆
与椭圆![]() “相似”.
“相似”.
(1)求经过点![]() ,且与椭圆
,且与椭圆![]() :
:![]() “相似”的椭圆
“相似”的椭圆![]() 的方程;
的方程;
(2)若![]() ,椭圆
,椭圆![]() 的离心率为
的离心率为![]() ,
,![]() 在椭圆
在椭圆![]() 上,过
上,过![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,且
两点,且![]() .
.
①若![]() 的坐标为
的坐标为![]() ,且
,且![]() ,求直线
,求直线![]() 的方程;
的方程;
②若直线![]() ,
,![]() 的斜率之积为
的斜率之积为![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某组织在某市征集志愿者参加志愿活动,现随机抽出60名男生和40名女生共100人进行调查,统计出100名市民中愿意参加志愿活动和不愿意参加志愿活动的男女生比例情况,具体数据如图所示.
(1)根据条件完成下列![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为愿意参与志愿活动与性别有关?
的把握认为愿意参与志愿活动与性别有关?

愿意 | 不愿意 | 总计 | |
男生 | |||
女生 | |||
总计 |
(2)现用分层抽样的方法从愿意参加志愿活动的市民中选取7名志愿者,再从中抽取2人作为队长,求抽取的2人至少有一名女生的概率.
参考数据及公式:
|
|
|
|
|
|
|
|
|
|
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,已知直角梯形ABCD中,![]() ,AB//DC,AB⊥AD,E为CD的中点,沿AE把△DAE折起到△PAE的位置(D折后变为P),使得PB=2,如图2.
,AB//DC,AB⊥AD,E为CD的中点,沿AE把△DAE折起到△PAE的位置(D折后变为P),使得PB=2,如图2.
(Ⅰ)求证:平面PAE⊥平面ABCE;
(Ⅱ)求点B到平面PCE的距离.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为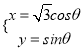 (
(![]() 为参数).在极坐标系(与平面直角坐标系
为参数).在极坐标系(与平面直角坐标系![]() 取相同的长度单位,且以原点
取相同的长度单位,且以原点![]() 为极点,以
为极点,以![]() 轴非负半轴为极轴)中,直线
轴非负半轴为极轴)中,直线![]() 的方程为
的方程为![]() .
.
(1)求曲线![]() 的普通方程及直线
的普通方程及直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() 是曲线
是曲线![]() 上的任意一点,求点
上的任意一点,求点![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,圆
中,圆![]() :
:![]() ,圆
,圆![]() :
:![]() .以坐标原点为极点,
.以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(2)设曲线![]() :
:![]() (
(![]() 为参数且
为参数且![]() ),
),![]() 与圆
与圆![]() ,
,![]() 分别交于
分别交于![]() ,
,![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(Ⅰ)若![]() 的图像在
的图像在![]() 处的切线过点
处的切线过点![]() ,求
,求![]() 的值并讨论
的值并讨论![]() 在
在![]() 上的单调增区间;
上的单调增区间;
(Ⅱ)定义:若直线![]() 与曲线
与曲线![]() 、
、![]() 都相切,则我们称直线
都相切,则我们称直线![]() 为曲线
为曲线![]() 、
、![]() 的公切线.若曲线
的公切线.若曲线![]() 与
与![]() 存在公切线,试求实数
存在公切线,试求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com