
已知函数g(x)=aln x·f(x)=x3 +x2+bx
(1)若f(x)在区间[1,2]上不是单调函数,求实数b的范围;
(2)若对任意x∈[1,e],都有g(x)≥-x2+(a+2)x恒成立,求实数a的取值范围;
(3)当b=0时,设F(x)= ,对任意给定的正实数a,曲线y=F(x)上是否存在两点P,Q,使得△POQ是以O(O为坐标原点)为直角顶点的直角三角形,而且此三角形斜边中点在y轴上?请说明理由.
,对任意给定的正实数a,曲线y=F(x)上是否存在两点P,Q,使得△POQ是以O(O为坐标原点)为直角顶点的直角三角形,而且此三角形斜边中点在y轴上?请说明理由.
(1)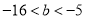 ;(2)
;(2) ;(3)详见解析.
;(3)详见解析.
【解析】
试题分析:(1)先求函数的导数,因为在区间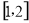 不单调,所以导函数的值不恒大于或小于0,即函数的最大值大于0,函数的最小值小于0,即不单调;
不单调,所以导函数的值不恒大于或小于0,即函数的最大值大于0,函数的最小值小于0,即不单调;
(2)根据条件化简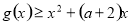 得,
得,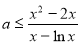 ,
,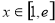 ,求出
,求出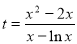 ,
,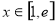 的最小值即可确定
的最小值即可确定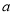 的范围,首先对函数求导,确定单调性,求出最值;
的范围,首先对函数求导,确定单调性,求出最值;
(3)先假设曲线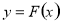 上存在两点
上存在两点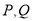 满足题意,设出
满足题意,设出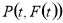
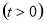 ,则
,则 ,从而由
,从而由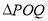 是以O(O为坐标原点)为直角顶点的直角三角形可建立关系式
是以O(O为坐标原点)为直角顶点的直角三角形可建立关系式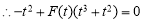 ,分情况求解即可.
,分情况求解即可.
试题解析:(1)由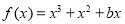
得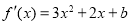 因
因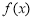 在区间[1,2]上不是单调函数
在区间[1,2]上不是单调函数
所以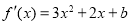 在[1,2]上最大值大于0,最小值小于0
在[1,2]上最大值大于0,最小值小于0
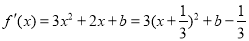
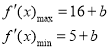 ∴
∴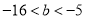 4分
4分
(2)由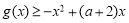 ,得
,得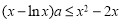 .
.
 ,且等号不能同时取,
,且等号不能同时取,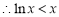 ,即
,即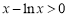
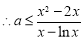 恒成立,即
恒成立,即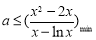 6分
6分
令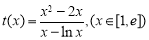 ,求导得,
,求导得,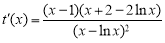 ,
,
当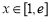 时,
时,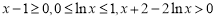 ,从而
,从而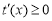 ,
,
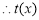 在
在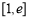 上为增函数,
上为增函数,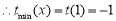 ,
,
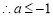 . 8分
. 8分
(3)由条件,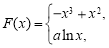
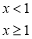 ,
,
假设曲线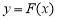 上存在两点
上存在两点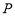 ,
,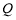 满足题意,则
满足题意,则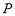 ,
,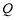 只能在
只能在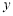 轴两侧, 9分
轴两侧, 9分
不妨设 ,则
,则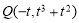 ,且
,且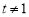 .
.
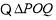 是以
是以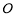 为直角顶点的直角三角形,
为直角顶点的直角三角形,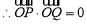 ,
,
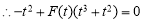 (*),
(*),
是否存在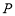 ,
,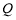 等价于方程
等价于方程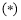 在
在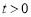 且
且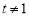 时是否有解.
时是否有解.
①若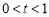 时,方程
时,方程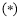 为
为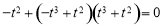 ,化简得
,化简得 ,此方程无解; 12分
,此方程无解; 12分
②若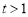 时,方程
时,方程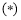 为
为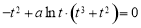 ,即
,即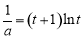 ,
,
设 ,则
,则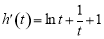 ,
,
显然,当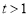 时,
时,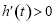 ,即
,即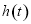 在
在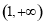 上为增函数,
上为增函数,
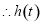 的值域为
的值域为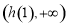 ,即
,即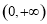 ,
,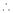 当
当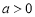 时,方程(*)总有解.
时,方程(*)总有解.
 对任意给定的正实数
对任意给定的正实数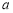 ,曲线
,曲线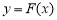 上总存在两点
上总存在两点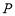 ,
,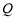 ,使得
,使得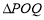 是以
是以 (
(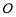 为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在
为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在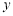 轴上. 14分
轴上. 14分
考点:1.利用导数求最大,最小值;2.导数的综合应用.


科目:高中数学 来源:2013-2014学年江西省盟校高三第二次联考理科数学试卷(解析版) 题型:选择题
以下四个命题中:
①从匀速传递的产品生产流水线上,质检员每10分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样;
②两个随机变量的线性相关性越强,相关系数的绝对值越接近于1;
③某项测量结果ξ服从正态分布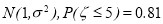 ,则
,则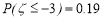 ;
;
④对于两个分类变量X与Y的随机变量k2的观测值k来说,k越小,判断“X与Y有关系”的把握程度越大.以上命题中其中真命题的个数为( )
A.4 B.3 C.2 D.1
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省盟校高三第一次联考理科数学试卷(解析版) 题型:选择题
如图,函数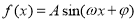 (其中
(其中 ,
,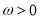 ,
,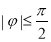 )与坐标轴的三个交点
)与坐标轴的三个交点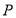 、
、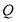 、
、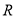 满足
满足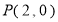 ,
,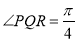 ,
, 为
为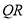 的中点,
的中点,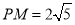 ,则
,则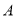 的值为( )
的值为( )

A.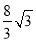 B.
B.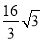 C.8 D.16
C.8 D.16
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省盟校高三第一次联考文科数学试卷(解析版) 题型:填空题
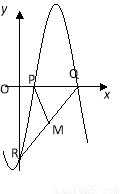
如图,函数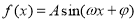 (其中
(其中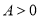 ,
,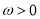 ,
,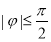 )与坐标轴的三个交点
)与坐标轴的三个交点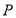 、
、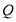 、
、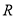 满足
满足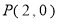 ,
,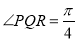 ,
,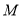 为
为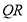 的中点,
的中点,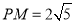 , 则
, 则 的值为____________
的值为____________
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省盟校高三第一次联考文科数学试卷(解析版) 题型:选择题
如图,一个四棱锥的底面为正方形,其三视图如图所示,则这个四棱锥的体积为( )

A、1 B、2 C、3 D、4
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省宜春市高三考前模拟理科数学试卷(解析版) 题型:解答题
在△ABC中,a、b、c分别为角A、B、C所对的边,且(2b+c)cosA十acosC =0。
(1)求角A的大小;
(2)求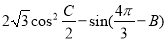 的最大值,并求取得最大值时角B、C的大小.
的最大值,并求取得最大值时角B、C的大小.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省宜春市高三考前模拟理科数学试卷(解析版) 题型:选择题
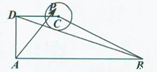
如图,在直角梯形ABCD中,AB⊥AD,AD=DC=1,AB=3,动点P在以点C为圆心且直线BD相切的圆内运动,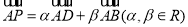 ,则
,则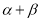 的取值范围是( )
的取值范围是( )
A.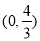 B.
B.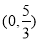 C.
C.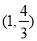 D.
D.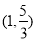
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省南昌市高三第二次模拟考试文科数学试卷(解析版) 题型:解答题
某公司生产产品A,产品质量按测试指标分为:指标大于或等于90为一等品,大于或等于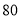 小于
小于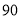 为二等品,小于
为二等品,小于 为三等品,生产一件一等品可盈利50元,生产一件二等品可盈利
为三等品,生产一件一等品可盈利50元,生产一件二等品可盈利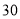 元,生产一件三等品亏损10元.现随机抽查熟练工人甲和新工人乙生产的这种产品各100件进行检测,检测结果统计如下:
元,生产一件三等品亏损10元.现随机抽查熟练工人甲和新工人乙生产的这种产品各100件进行检测,检测结果统计如下:
测试指标 |
|
|
|
|
|
|
甲 | 3 | 7 | 20 | 40 | 20 | 10 |
乙 | 5 | 15 | 35 | 35 | 7 | 3 |
根据上表统计得到甲、乙两人生产产品A为一等品、二等品、三等品的频率分别估计为他们生产产品A为一等品、二等品、三等品的概率.
(1)计算甲生产一件产品A,给工厂带来盈利不小于30元的概率;
(2)若甲一天能生产20件产品A,乙一天能生产15件产品A,估计甲乙两人一天生产的35件产品A中三等品的件数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com