
【题目】设函数![]() ,
, ![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的极小值;
的极小值;
(2)讨论函数![]() 零点的个数;
零点的个数;
(3)若对任意的![]() ,
, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)极小值2;(2)![]()
【解析】试题分析:(Ⅰ)代入![]() ,求得
,求得![]() ,得到
,得到![]() 和
和![]() 的解集,得出函数的单调性,即可求解函数的极小值;
的解集,得出函数的单调性,即可求解函数的极小值;
(Ⅱ)由题意得![]() ,令
,令![]() ,得
,得![]() ,设
,设![]() ,求得
,求得![]() ,得到
,得到![]() 的单调性,得到
的单调性,得到![]() 的最大值,分类讨论,即可求解零点的个数;
的最大值,分类讨论,即可求解零点的个数;
(Ⅲ)由题意原命题等价于![]() 恒成立,设
恒成立,设![]() ,进而转化为
,进而转化为![]() 在
在![]() 上单调递减,利用导数,即可求得实数
上单调递减,利用导数,即可求得实数![]() 的取值范围.
的取值范围.
试题解析:
(1)因为![]() ,所以当
,所以当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上单调递减;当
上单调递减;当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上单调递增;
上单调递增;
所以当![]() 时,
时, ![]() 取得极小值
取得极小值![]() .
.
(2)![]()
![]()
![]() ,
,
令![]() ,得
,得![]() .
.
设![]() ,则
,则![]()
![]() .
.
所以当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上单调递减;
上单调递减;
所以![]() 的最大值为
的最大值为![]() ,又
,又![]() ,可知:
,可知:
①当![]() 时,函数
时,函数![]() 没有零点;②当
没有零点;②当![]() 或
或![]() 时,函数
时,函数![]() 有且仅有1个零点;
有且仅有1个零点;
③当![]() 时,函数
时,函数![]() 有2个零.
有2个零.
(3)原命题等价于![]() 恒成立.
恒成立. ![]() .
.
设![]()
![]() ,
,
则![]() 等价于
等价于![]() 在
在![]() 上单调递减.
上单调递减.
即![]() 在
在![]() 上恒成立,
上恒成立,
所以![]()
![]()
![]() 恒成立,所以
恒成立,所以![]() .
.
即![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
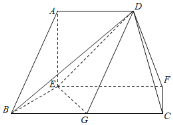
【题目】在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点.
(Ⅰ)求证:AB∥平面DEG;
(Ⅱ)求二面角C-DF-E的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x|(x﹣a),a为实数.
(1)若函数f(x)为奇函数,求实数a的值;
(2)若函数f(x)在[0,2]为增函数,求实数a的取值范围;
(3)是否存在实数a(a<0),使得f(x)在闭区间![]() 上的最大值为2,若存在,求出a的值;若不存在,请说明理由.
上的最大值为2,若存在,求出a的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产甲、乙两种产品均需要![]() ,
,![]() 两种原料,已知生产1吨每种产品所需原料及每天原料的可用限额如表所示.如果生产1吨甲、乙产品可获得利润分别为3万元、4万元,则该企业每天可获得最大利润为( )
两种原料,已知生产1吨每种产品所需原料及每天原料的可用限额如表所示.如果生产1吨甲、乙产品可获得利润分别为3万元、4万元,则该企业每天可获得最大利润为( )
甲 | 乙 | 原料限额 | |
| 3 | 2 | 10 |
| 1 | 2 | 6 |
A. 10万元B. 12万元C. 13万元D. 14万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sin2x-2sin2x-a.
①若f(x)=0在x∈R上有解,则a的取值范围是______;
②若x1,x2是函数y=f(x)在[0,![]() ]内的两个零点,则sin(x1+x2)=______
]内的两个零点,则sin(x1+x2)=______
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)若函数![]() 为偶函数,求实数
为偶函数,求实数![]() 的值;
的值;
(2)若![]() ,
,![]() ,且函数
,且函数![]() 在
在![]() 上是单调函数,求实数
上是单调函数,求实数![]() 的值;
的值;
(3)若![]() ,若当
,若当![]() 时,总有
时,总有![]() ,使得
,使得![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求![]() 的最小正周期;
的最小正周期;
(2)当![]() 时,
时,
(ⅰ)求函数![]() 的单调递减区间;
的单调递减区间;
(ⅱ)求函数![]() 的最大值最小值,并分别求出使该函数取得最大值最小值时的自变量
的最大值最小值,并分别求出使该函数取得最大值最小值时的自变量![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着我国经济的发展,居民收入逐年增长.某地区2014年至2018年农村居民家庭人均纯收入![]() (单位:千元)的数据如下表:
(单位:千元)的数据如下表:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代号 | 1 | 2 | 3 | 4 | 5 |
人均纯收入 | 5 | 4 | 7 | 8 | 10 |
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)利用(1)中的回归方程,分析2014年至2018年该地区农村居民家庭人均纯收入的变化情况,并预测2019年该地区农村居民家庭人均纯收入为多少?
附:回归直线的斜率和截距的最小二乘估计公式分别为 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com