
(14分)如图,在三棱锥S—ABC中, 是边长为4的正三角形,平面SAC⊥平面ABC,SA =" SC" =
是边长为4的正三角形,平面SAC⊥平面ABC,SA =" SC" = ,M、N分别为AB、SB的中点。
,M、N分别为AB、SB的中点。

⑴ 求证:AC⊥SB;
⑵ 求二面角N—CM—B的正切值;
⑶ 求点B到平面CMN的距离。
⑴取AC中点O,连结OS、OB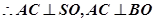 ∴SO⊥平面ABC,SO⊥BO如图建立空间直角坐标系O—xyz
∴SO⊥平面ABC,SO⊥BO如图建立空间直角坐标系O—xyz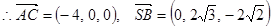
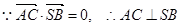 ⑵
⑵ 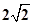 ⑶
⑶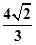
【解析】
试题分析:⑴ 取AC中点O,连结OS、OB
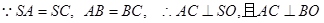
∵平面 平面ABC,平面SAC
平面ABC,平面SAC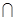 平面ABC=AC
平面ABC=AC
∴SO⊥平面ABC, SO⊥BO
如图建立空间直角坐标系O—xyz
则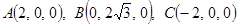
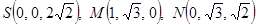
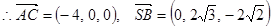
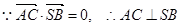
⑵ 由⑴得
设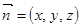 为平面CMN的一个法向量,则
为平面CMN的一个法向量,则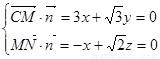 ,取
,取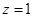
则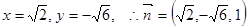
又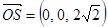 为平面ABC的一个法向量
为平面ABC的一个法向量
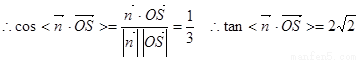
⑶ 由⑴⑵得 为平面CMN的一个法向量
为平面CMN的一个法向量
∴点B到平面CMN的距离 ……14分
……14分
考点:线线垂直的判定,二面角点面距的计算
点评:本题的关键是由已知条件找到建立空间直角坐标系的合适位置,进而找到相关点,向量的坐标,代入线面角点面距的向量计算公式求解,有一定的难度


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源:2011-2012学年浙江省温州市高三第一次适应性测试理科数学 题型:解答题
(本题满分14分)如图,在三棱锥 中,
中,
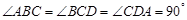 ,
,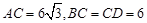 ,
,
设顶点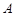 在底面
在底面 上的射影为
上的射影为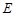 .
.
(Ⅰ)求证: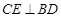 ;
;
(Ⅱ)设点 在棱
在棱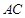 上,且
上,且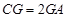 ,
,
试求二面角 的余弦值
的余弦值
查看答案和解析>>
科目:高中数学 来源:2011-2012学年北京市丰台区高三上学期期末考试理科数学 题型:解答题
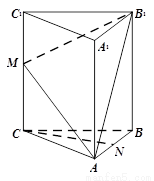
(本小题共14分)如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=BC=2,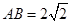 ,CC1=4,M是棱CC1上一点.
,CC1=4,M是棱CC1上一点.
(Ⅰ)求证:BC⊥AM;
(Ⅱ)若M,N分别是CC1,AB的中点,求证:CN //平面AB1M;
(Ⅲ)若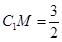 ,求二面角A-MB1-C的大小.
,求二面角A-MB1-C的大小.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年北京市丰台区高三上学期期末考试文科数学 题型:解答题
(本小题共14分)如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=BC,M,N分别是CC1,AB的中点.
(Ⅰ)求证:CN⊥AB1;
(Ⅱ)求证:CN //平面AB1M.

查看答案和解析>>
科目:高中数学 来源:2013届北京市高二上学期期中考试理科数学 题型:解答题
(本题满分14分)如图,在三棱柱 中,
中,
每个侧面均为正方形, 为底边
为底边 的中点,
的中点, 为侧棱
为侧棱 的中点.
的中点.
(Ⅰ)求证: ∥平面
∥平面 ;
;
(Ⅱ)求证: 平面
平面 ;
;
(Ⅲ)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.

查看答案和解析>>
科目:高中数学 来源:烟台市英文学校2010高三一模考试理科数学试题 题型:解答题
(本小题满分14分)
如图,在三棱柱 中,侧面
中,侧面 底面ABC,
底面ABC, ,
, ,且
,且 为AC中点.
为AC中点. 
(I)证明: 平面ABC;
平面ABC;
(II)求直线 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(III)在 上是否存在一点E,使得
上是否存在一点E,使得 平面
平面 ,若不存在,说明理由;若存在,确定点E的位置.
,若不存在,说明理由;若存在,确定点E的位置.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com