
如图,在棱长为1的正方体![]() 中.
中.
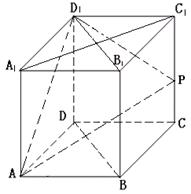
(I)在侧棱![]() 上是否存在一个点P,使得直线
上是否存在一个点P,使得直线![]() 与平面
与平面![]() 所成角的正切值为
所成角的正切值为![]() ;
; ![]()
![]()
(Ⅱ)若P是侧棱![]() 上一动点,在线段
上一动点,在线段![]() 上是否存在一个定点
上是否存在一个定点![]() ,使得
,使得![]() 在平面
在平面![]() 上的射影垂直于
上的射影垂直于![]() .并证明你的结论.
.并证明你的结论.
(1)当PC=![]() 时,直线AP与平面
时,直线AP与平面![]() 所成的角的正切值为
所成的角的正切值为![]() .(2)点Q应当是A1C1的中点O1,
.(2)点Q应当是A1C1的中点O1,
解法一:(Ⅰ)如图,设PC=m,连AC,
设AC与BD相交于点O,AP与平面![]() 相交于点G,,
相交于点G,,
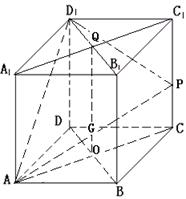
连结OG,因为PC∥平面![]() ,
,
平面![]() ∩平面APC=OG,故OG∥PC,
∩平面APC=OG,故OG∥PC,
所以,OG=![]() PC=
PC=![]() .又AO⊥BD,AO⊥BB1,
.又AO⊥BD,AO⊥BB1,
所以AO⊥平面![]() ,
,
故∠AGO是AP与平面![]() 所成的角.
所成的角.
在Rt△AOG中,tan![]() AGO=
AGO= ,
, ![]() 即m=
即m=![]() .
.
所以,当PC=![]() 时,直线AP与平面
时,直线AP与平面![]() 所成的角的正切值为
所成的角的正切值为![]() . …………………6分
. …………………6分
(Ⅱ)可以推测,点Q应当是A1C1的中点O1,因为D1O1⊥A1C1, 且 D1O1⊥A1A ,所以 D1O1⊥平面ACC1A1,又AP![]() 平面ACC1A1,故 D1O1⊥AP.那么根据三垂线定理知,D1O1在平面APD1的射影与AP垂直. …………………12分
平面ACC1A1,故 D1O1⊥AP.那么根据三垂线定理知,D1O1在平面APD1的射影与AP垂直. …………………12分
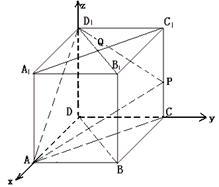
解法二:(Ⅰ)建立如图所示的空间直角坐标系,
则A(1,0,0),B(1,1,0),P(0,1,m),C(0,1,0),D(0,0,0),
B1(1,1,1),D1(0,0,1)
所以![]()
![]()
![]()
又由![]() 知,
知,![]() 为平面
为平面![]() 的一个法向量.
的一个法向量.
设AP与平面![]() 所成的角为
所成的角为![]() ,
,
则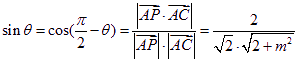 。
。
依题意有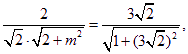
解得![]() .
.
故当![]() 时,直线AP与平面
时,直线AP与平面![]() 所成的角的正切值为
所成的角的正切值为![]() . ……………6分
. ……………6分
(Ⅱ)若在A1C1上存在这样的点Q,设此点的横坐标为![]() ,
,
则Q(x,1-![]() ,1),
,1),![]() 。
。
依题意,要使D1Q在平面APD1上的射影垂直于AP,
等价于D1Q⊥AP![]()
即Q为A1C1的中点时,满足题设要求. …………………12分 ![]()
![]()


科目:高中数学 来源: 题型:
 如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.查看答案和解析>>
科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.查看答案和解析>>
科目:高中数学 来源:2009-2010学年江苏省南京市金陵中学高三(上)8月月考数学试卷(解析版) 题型:解答题

查看答案和解析>>
科目:高中数学 来源:2012年安徽省合肥八中高考数学一模试卷(理科)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com