

 ),试用θ表示出总施工费用y(万元)的解析式,并求y的最小值.
),试用θ表示出总施工费用y(万元)的解析式,并求y的最小值. ,所以CE=EB=
,所以CE=EB= ,ED=tanθ,AE=
,ED=tanθ,AE= -tanθ.(7分)则y=2×
-tanθ.(7分)则y=2×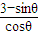 +2
+2 ,令
,令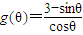 ,则g′(θ)=
,则g′(θ)=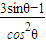 ,由此能求出施工总费用的最小值.
,由此能求出施工总费用的最小值. ,AB=2,
,AB=2,
 +2×0.5=5+
+2×0.5=5+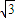 .(万元) …(6分)
.(万元) …(6分) ,
,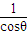 ,ED=tanθ,AE=
,ED=tanθ,AE=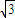 -tanθ.(7分)
-tanθ.(7分)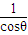 ×4+
×4+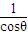 ×2+(
×2+(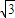 -tanθ)×2
-tanθ)×2 +2
+2 ,(9分)
,(9分)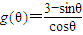 ,
,
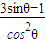 ,(10分)
,(10分) ,所以0
,所以0 ,
,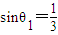 ,
, ,
, ,即0≤θ<θ1时,g′(θ)<0,
,即0≤θ<θ1时,g′(θ)<0,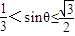 ,即
,即 时,g′(x)>0,
时,g′(x)>0,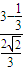 =2
=2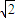 ,
, +2
+2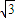 ,(12分)
,(12分) ,
,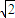 +2
+2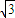 )万元,其中ED=
)万元,其中ED= .(13分)
.(13分)

科目:高中数学 来源: 题型:

| P | 3 |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年福建省福州市高三质量检测理科数学 题型:解答题
(本小题满分1 3分)
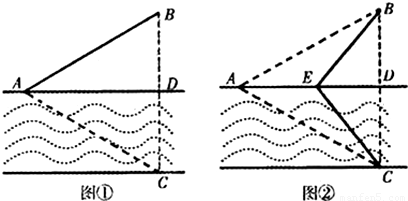
如图①,一条宽为l km的两平行河岸有村庄A和供电站C,村庄B与A、C的直线距离都是2km,BC与河岸垂直,垂足为D.现要修建电缆,从供电站C向村庄A、B供电.修建地下电缆、水下电缆的费用分别是2万元/km、4万元/km.
(Ⅰ)已知村庄A与B原来铺设有旧电缆仰,需要改造,旧电缆的改造费用是0.5万元/km.现
决定利用旧电缆修建供电线路,并要求水下电缆长度最短,试求该方案总施工费用的最小值.
(Ⅱ)如图②,点E在线段AD上,且铺设电缆的线路为CE、EA、EB.若∠DCE=θ (0≤θ≤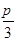 ),试用θ表示出总施工费用y(万元)的解析式,并求y的最小值.
),试用θ表示出总施工费用y(万元)的解析式,并求y的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:

(第20题图)
(1)若平板车卡在直角走廊内,且∠CAB=θ,试求平板面的长l;
(2)若平板车要想顺利通过直角走廊,其长度不能超过多少米?
查看答案和解析>>
科目:高中数学 来源:2013年高考数学复习卷C(六)(解析版) 题型:解答题
 ),试用θ表示出总施工费用y(万元)的解析式,并求y的最小值.
),试用θ表示出总施工费用y(万元)的解析式,并求y的最小值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com