七星图书口算速算天天练系列答案
初中学业考试导与练系列答案科目：高中数学 来源：2014年高考数学（文）二轮复习专题提升训练江苏专用阶段检测5练习卷（解析版） 题型：解答题
如图，在边长为4的菱形ABCD中，∠DAB＝60°，点E、F分别在边CD、CB上，点E与点C、D不重合，EF⊥AC，EF∩AC＝O，沿EF将△CEF翻折到△PEF的位置，使平面PEF⊥平面ABFED.
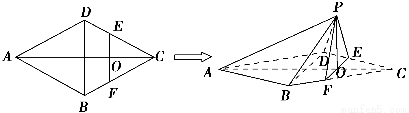
(1)求证：BD⊥平面POA；
(2)记三棱锥P ?ABD体积为V1，四棱锥P ?BDEF体积为V2，且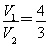
，求此时线段PO的长．
查看答案和解析>>
科目：高中数学 来源：2014年高考数学（文）二轮复习专题提升训练江苏专用阶段检测3练习卷（解析版） 题型：解答题
已知等差数列{an}满足：a2＝5，a4＋a6＝22，数列{bn}满足b1＋2b2＋…＋2n－1bn＝nan，设数列{bn}的前n项和为Sn.
(1)求数列{an}，{bn}的通项公式；
(2)求满足13<Sn<14的n的集合．
查看答案和解析>>
科目：高中数学 来源：2014年高考数学（文）二轮复习专题提升训练江苏专用阶段检测2练习卷（解析版） 题型：解答题
如图，游客从某旅游景区的景点A处下山至C处有两种路径．一种是从A沿直线步行到C，另一种是先从A沿索道乘缆车到B，然后从B沿直线步行到C.现有甲、乙两位游客从A处下山，甲沿AC匀速步行，速度为50 m/min.在甲出发2 min后，乙从A乘缆车到B，在B处停留1 min后，再从B匀速步行到C.假设缆车匀速直线运动的速度为130 m/min，山路AC长为1 260 m，经测量cos A＝
，cos C＝
.
(1)求索道AB的长；
(2)问乙出发多少分钟后，乙在缆车上与甲的距离最短？
(3)为使两位游客在C处互相等待的时间不超过3分钟，乙步行的速度应控制在什么范围内？
查看答案和解析>>
科目：高中数学 来源：2014年高考数学（文）二轮复习专题提升训练江苏专用阶段检测2练习卷（解析版） 题型：填空题
已知f(x)＝sin x，x∈R，g(x)的图象与f(x)的图象关于点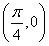
对称，则在区间[0,2π]上满足f(x)≤g(x)的x的范围是________．
查看答案和解析>>
科目：高中数学 来源：2014年高考数学（文）二轮复习专题提升训练江苏专用阶段检测1练习卷（解析版） 题型：解答题
某厂生产某种产品的年固定成本为250万元，每生产x千件，需另投入成本为C(x)．当年产量不足80千件时，C(x)＝
x2＋10x(万元)；当年产量不小于80千件时，C(x)＝51x＋
－1 450(万元)，每件商品售价为0.05万元，通过市场分析，该厂生产的商品能全部售完．
(1)写出年利润L(万元)关于年产量x(千件)的函数解析式；
(2)当年产量为多少千件时，该厂在这一商品的生产中所获利润最大？
查看答案和解析>>
科目：高中数学 来源：2014年高考数学（文）二轮复习专题提升训练江苏专用9练习卷（解析版） 题型：解答题
知数列{an}是首项为
，公比为
的等比数列，设bn＋15log3an＝t，常数t∈N*.
(1)求证：{bn}为等差数列；
(2)设数列{cn}满足cn＝anbn，是否存在正整数k，使ck，ck＋1，ck＋2按某种次序排列后成等比数列？若存在，求k，t的值；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源：2014年高考数学（文）二轮复习专题提升训练江苏专用6练习卷（解析版） 题型：填空题
已知函数f(x)＝Acos(ωx＋φ)(A>0，ω>0，φ∈R)，则“f(x)是奇函数”是“φ＝
”的______条件．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
