
 )的导函数
)的导函数 的部分图像如图所示,其中,P为图像与y轴的交点,A,C为图像与x轴的两个交点,B为图像的最低点.
的部分图像如图所示,其中,P为图像与y轴的交点,A,C为图像与x轴的两个交点,B为图像的最低点.
 ,点P的坐标为(0,
,点P的坐标为(0, ),则
),则 ;
;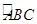 与x轴所围成的区域内随机取一点,则该点在△ABC内的概率为 .
与x轴所围成的区域内随机取一点,则该点在△ABC内的概率为 .
 ,f′(0)=
,f′(0)= 代入导函数解析式,即可解得ω的值;(2)先利用定积分的几何意义,求曲线段
代入导函数解析式,即可解得ω的值;(2)先利用定积分的几何意义,求曲线段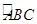 与x轴所围成的区域面积,再求三角形ABC的面积,最后利用几何概型概率计算公式求面积之比即可得所求概率。解:(1)∵函数f(x)="sin" (ωx+φ)的导函数y=f′(x)=ωcos(ωx+φ),其中
与x轴所围成的区域面积,再求三角形ABC的面积,最后利用几何概型概率计算公式求面积之比即可得所求概率。解:(1)∵函数f(x)="sin" (ωx+φ)的导函数y=f′(x)=ωcos(ωx+φ),其中 ,过点P(0,
,过点P(0, ),∴ωcos
),∴ωcos =
= ∴ω=3,故答案为 3,
∴ω=3,故答案为 3,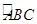 与x轴所围成的区域面积为
与x轴所围成的区域面积为 ,三角形ABC的面积为
,三角形ABC的面积为 ,∴在曲线段
,∴在曲线段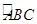 与x轴所围成的区域内随机取一点,则该点在△ABC内的概率为
与x轴所围成的区域内随机取一点,则该点在△ABC内的概率为 ,故答案为3,
,故答案为3,


科目:高中数学 来源:不详 题型:填空题

 ,有下列命题:
,有下列命题: 为奇函数.
为奇函数. 的最小正周期为2
的最小正周期为2 .
. 的图像关于直线
的图像关于直线 对称,其中正确的命题序号为_____________.
对称,其中正确的命题序号为_____________.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com