
【题目】设常数![]() ,函数
,函数![]() .
.
(1)令![]() 时,求
时,求![]() 的最小值,并比较
的最小值,并比较![]() 的最小值与零的大小;
的最小值与零的大小;
(2)求证:![]() 在
在![]() 上是增函数;
上是增函数;
(3)求证:当![]() 时,恒有
时,恒有![]() .
.
【答案】(1)最小值为![]() ,最小值大于零.(2)证明见解析.(3)证明见解析
,最小值大于零.(2)证明见解析.(3)证明见解析
【解析】
(1)对函数![]() 进行求导,确定函数
进行求导,确定函数![]() 的解析式,再对函数
的解析式,再对函数![]() 求导,列表判断出该函数的单调性以及极值,最后确定函数
求导,列表判断出该函数的单调性以及极值,最后确定函数![]() 的最小值,再判断
的最小值,再判断![]() 的最小值与零的大小即可;
的最小值与零的大小即可;
(2)利用(1)中的结论,可以判断出函数![]() 的正负性,进而能证明出
的正负性,进而能证明出![]() 的单调性;
的单调性;
(3)利用(2)中的结论进行证明即可.
(1)因为![]() ,
,
所以![]() .
.
所以![]() ,
,
所以![]() ,令
,令![]() ,得
,得![]() .
.
列表如下:
|
| 2 |
|
|
| 0 |
|
| 减 | 极小值 | 增 |
所以![]() 在
在![]() 处取得极小值
处取得极小值![]() ,
,
即![]() 的最小值为
的最小值为![]() ,
,
因为![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() 即
即![]() 的最小值大于零.
的最小值大于零.
(2)由(1)知,![]() 的最小值为正数,
的最小值为正数,
所以对一切![]() ,恒有
,恒有![]() .
.
从而当![]() 时,恒有
时,恒有![]() ,故
,故![]() 在
在![]() 上是增函数.
上是增函数.
(3)由(2)知![]() 在
在![]() 上是增函数,
上是增函数,
所以当![]() 时,
时,![]() .
.
又![]() ,
,
所以![]() ,即
,即![]() ,
,
所以![]() ,
,
故当![]() 时,恒有
时,恒有![]() .
.


科目:高中数学 来源: 题型:
【题目】雅山中学采取分层抽样的方法从应届高三学生中按照性别抽出20名学生作为样本,其选报文科理科的情况如下表所示.
男 | 女 | |
文科 | 2 | 5 |
理科 | 10 | 3 |
(Ⅰ)若在该样本中从报考文科的学生中随机地选出3人召开座谈会,试求3人中既有男生也有女生的概率;
(Ⅱ)用假设检验的方法分析有多大的把握认为雅山中学的高三学生选报文理科与性别有关?
参考公式和数据:![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.07 | 2.71 | 3.84 | 5.02 | 6.64 | 7.88 | 10.83 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为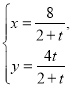 (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若射线![]() (
(![]() )与直线
)与直线![]() 和曲线
和曲线![]() 分别交于
分别交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图是一个![]() 的方格(其中心的方格线已被划去).一只青蛙停在
的方格(其中心的方格线已被划去).一只青蛙停在![]() 格处,从某一时刻起,青蛙每隔一秒钟就跳到与它所在方格有公共边的另一方格内,直至跳到
格处,从某一时刻起,青蛙每隔一秒钟就跳到与它所在方格有公共边的另一方格内,直至跳到![]() 格才停下..若青蛙经过每一个方格不超过一次,则青蛙的跳法总数为________.
格才停下..若青蛙经过每一个方格不超过一次,则青蛙的跳法总数为________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高考改革后,学生除了语数外三门必选外,可在A类科目:物理、化学、生物和B类科目:政治、地理、历史共6个科目中任选3门.
(1)若小明同学已经确定选了物理,现在他还要从剩余的5科中再选2科,则他在历史与地理两科中至少选一科的概率?
(2)求小明同学选A类科目数X的分布列、数学期望和方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图![]() ,在边长为
,在边长为![]() 的菱形
的菱形![]() 中,
中,![]() ,现沿对角线
,现沿对角线![]() 把
把![]() 翻折到
翻折到![]() 的位置得到四面体
的位置得到四面体![]() ,如图
,如图![]() 所示.已知
所示.已知![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() 是线段
是线段![]() 上的点,且
上的点,且![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com