分析:(I)法一:几何法:要D1E⊥平面AB1F,先确定D1E⊥平面AB1F内的两条相交直线,由三垂线定理易证D1E⊥AB1,同理证明D1E⊥AF即可.
法二:代数法:建立空间直接坐标系,运用空间向量的数量积等于0,来证垂直.
(II)法一:求二面角C1-EF-A的大小,转化为求C1-EF-C的大小,利用三垂线定理方法:E、F都是所在线的中点,
过C连接AC,设AC与EF交于点H,则CH⊥EF,连接C1H,则CH是C1H在底面ABCD内的射影.
∠C1HC是二面角C1-EF-C的平面角.求解即可.
法二:找出两个平面的法向量,运用空间向量数量积公式求出二面角的余弦值,再求其角.
解答: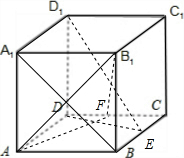
解法一:(I)连接A
1B,则A
1B是D
1E在面ABB
1A;内的射影
∵AB
1⊥A
1B,∴D
1E⊥AB
1,
于是D
1E⊥平面AB
1F?D
1E⊥AF.
连接DE,则DE是D
1E在底面ABCD内的射影.
∴D
1E⊥AF?DE⊥AF.
∵ABCD是正方形,E是BC的中点.
∴当且仅当F是CD的中点时,DE⊥AF,
即当点F是CD的中点时,D
1E⊥平面AB
1F.(6分)
(II)当D
1E⊥平面AB
1F时,由(I)知点F是CD的中点.
又已知点E是BC的中点,连接EF,则EF∥BD.连接AC,
设AC与EF交于点H,则CH⊥EF,连接C
1H,则CH是
C
1H在底面ABCD内的射影.
C
1H⊥EF,即∠C
1HC是二面角C
1-EF-C的平面角.
在Rt△C
1CH中,∵C
1C=1,CH=
AC=
,
∴tan∠C
1HC=
==2.
∴∠C
1HC=arctan
2,从而∠AHC
1=π-arctan2
.
故二面角C
1-EF-A的大小为
π-arctan2.
解法二:以A为坐标原点,建立如图所示的空间直角坐标系
(1)设DF=x,则A(0,0,0),B(1,0,0),D(0,1,0),
A
1(0,0,1),B(1,0,1),D
1(0,1,1),E
(1,,0),F(x,1,0)∴
=(1,-,-1),=(1,0,1),=(x,1,0)∴
•=1-1=0,即D
1E⊥AB
1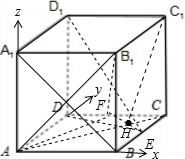
于是D
1E⊥平面AB
1F?D
1E∪AF?
•=0?x-=0即x=
.故当点F是CD的中点时,D
1E⊥平面AB
1F
(2)当D
1E⊥平面AB
1F时,F是CD的中点,又E是BC的中点,连接EF,则EF∥BD.
连接AC,设AC与EF交于点H,则AH⊥EF.连接C
1H,则CH是C
1H在底面ABCD内的射影.
∴C
1H⊥EF,即∠AHC
1是二面角C
1-EF-A的平面角.
∵
C1(1,1,1),H(,,0),
∵
=(,,1),=(-,-,0).
∴
cos∠AHC1=,
=
=-,
即
∠AHC1=arccos(-)=π-arccos.
故二面角C
1-EF-A的大小为π-arccos
.
点评:本小题主要考查线面关系和正方体等基础知识,考查空间想象能力和推理运算能力.空间向量计算法容易出错.

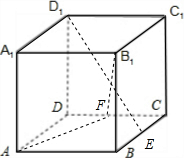 如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E是棱BC的中点,点F是棱CD上的动点.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E是棱BC的中点,点F是棱CD上的动点. 解法一:(I)连接A1B,则A1B是D1E在面ABB1A;内的射影
解法一:(I)连接A1B,则A1B是D1E在面ABB1A;内的射影


 阅读快车系列答案
阅读快车系列答案 如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
 如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
