
已知某海滨浴场的海浪高达y(米)是时间t(0≤t≤24,单位:小时)的函数,记作y=f(t).下表是某日各时的浪高数据.
| t(时) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y(米) | 1.5 | 1.0 | 0.5 | 1.0 | 1.5 | 1.0 | 0.5 | 0.99 | 1.5 |
(1) y=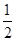 cos
cos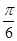 t+1.
t+1.
(2)在规定时间上午8:00至晚上2:00之间,有6个小时时间可供冲浪者运动,即上午9:00至下午15:00.
解析试题分析:(1)由表中数据,知周期T=12,
∵ω=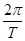 =
=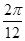 =
=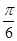 .
.
由t=0,y=1.5,得A+b=1.5.
由t=3,y=1.0,得b=1.0.
∴A=0.5,b=1,∴振幅为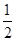 ,
,
∴y=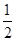 cos
cos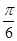 t+1.
t+1.
(2)由题意知,当y>1时才可对冲浪者开放.
∴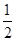 cos
cos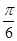 t+1>1,∴cos
t+1>1,∴cos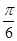 t>0.
t>0.
∴2kπ-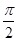 <
<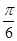 t<2kπ+
t<2kπ+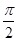 ,
,
即12k-3<t<12k+3.
∵0≤t≤24,故可令k分别为0、1、2,得0≤t<3或9<t<15或21<t≤24.
∴在规定时间上午8:00至晚上20:00之间,有6个小时时间可供冲浪者运动,即上午9:00至下午15:00.
考点:函数模型,三角函数的图象和性质。
点评:中档题,作为一道实际应用问题,首先应“审清题意,明确函数模型,解答数学问题”。余弦形函数的图像和性质,可类比正弦型函数的图象和性质加以研究。本题与不等式解法相结合,注意将数字转化成时刻。


科目:高中数学 来源: 题型:解答题
如图,倾斜角为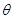 的直线
的直线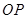 与单位圆在第一象限的部分交于点
与单位圆在第一象限的部分交于点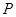 ,单位圆与坐标轴交于点
,单位圆与坐标轴交于点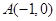 ,点
,点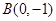 ,
,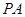 与
与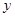 轴交于点
轴交于点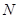 ,
, 与
与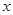 轴交于点
轴交于点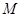 ,设
,设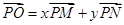
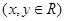
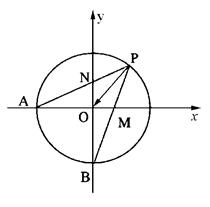
(1)用角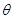 表示点
表示点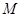 、点
、点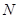 的坐标;
的坐标;
(2)求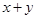 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com