
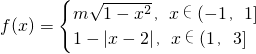 ,其中m为整数,若方程3f(x)-x=0恰好有5个解,则m=________.
,其中m为整数,若方程3f(x)-x=0恰好有5个解,则m=________. 与第二个椭圆相交,而与第三个椭圆不公共点.把直线分别代入椭圆方程,根据△可求得m的范围.
与第二个椭圆相交,而与第三个椭圆不公共点.把直线分别代入椭圆方程,根据△可求得m的范围.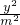 =1(y≥0),
=1(y≥0),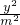 =1(y≥0)相交,
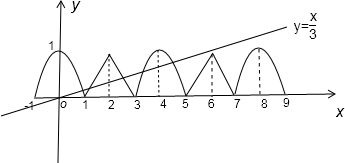
=1(y≥0)相交,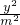 =1 (y≥0)无公共点时,方程恰有5个实数解,
=1 (y≥0)无公共点时,方程恰有5个实数解, 代入(x-4)2+
代入(x-4)2+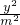 =1 (y≥0)得,(9m2+1)x2-72m2x+135m2=0,令t=9m2(t>0),
=1 (y≥0)得,(9m2+1)x2-72m2x+135m2=0,令t=9m2(t>0),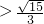 ,
, 与第三个椭圆(x-8)2+
与第三个椭圆(x-8)2+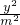 =1 (y≥0)由△<0可计算得 m<
=1 (y≥0)由△<0可计算得 m< ,
, ,
, ),故答案为m∈(
),故答案为m∈( ,
, ).
).


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:
|
| x |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| x |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源:2010年江西省赣州市于都县高考数学模拟试卷(文科)(解析版) 题型:解答题
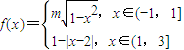 ,其中m为整数,若方程3f(x)-x=0恰好有5个解,则m= .
,其中m为整数,若方程3f(x)-x=0恰好有5个解,则m= .查看答案和解析>>
科目:高中数学 来源:2010年江西省赣州市于都县高考数学模拟试卷(理科)(解析版) 题型:解答题
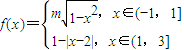 ,其中m为整数,若方程3f(x)-x=0恰好有5个解,则m= .
,其中m为整数,若方程3f(x)-x=0恰好有5个解,则m= .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com