
【题目】已知指数函数![]()
(1)函数![]() 过定点
过定点![]() ,求
,求![]() 的值;
的值;
(2)当![]() 时,求函数
时,求函数![]() 的最小值
的最小值![]() ;
;
(3)是否存在实数![]() ,使得(2)中关于
,使得(2)中关于![]() 的函数
的函数![]() 的定义域为
的定义域为![]() 时,值域为
时,值域为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源: 题型:
【题目】(1)求经过两直线2x-3y-3=0和x+y+2=0的交点且与直线3x+y-1=0平行的直线l的方程;
(2)求经过两直线l1:x-2y+4=0和l2:x+y-2=0的交点P,且与直线l3:3x-4y+5=0垂直的直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合![]() .对于
.对于![]() ,
, ![]() ,定义
,定义![]() 与
与![]() 之间的距离为
之间的距离为![]() .
.
(Ⅰ)写出![]() 中的所有元素,并求两元素间的距离的最大值;
中的所有元素,并求两元素间的距离的最大值;
(Ⅱ)若集合![]() 满足:
满足: ![]() ,且任意两元素间的距离均为2,求集合
,且任意两元素间的距离均为2,求集合![]() 中元素个数的最大值并写出此时的集合
中元素个数的最大值并写出此时的集合![]() ;
;
(Ⅲ)设集合![]() ,
, ![]() 中有
中有![]() 个元素,记
个元素,记![]() 中所有两元素间的距离的平均值为
中所有两元素间的距离的平均值为![]() ,证明
,证明![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,且离心率为
,且离心率为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点,以
两点,以![]() 为对角线作正方形
为对角线作正方形![]() ,记直线
,记直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,问
,问![]() 、
、![]() 两点间距离是否为定值?如果是,求出定值;如果不是,请说明理由.
两点间距离是否为定值?如果是,求出定值;如果不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知幂函数![]() 满足
满足![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)若函数![]() ,是否存在实数
,是否存在实数![]() 使得
使得![]() 的最小值为0?若存在,求出
的最小值为0?若存在,求出![]() 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(3)若函数![]() ,是否存在实数
,是否存在实数![]() ,使函数
,使函数![]() 在
在![]() 上的值域为
上的值域为![]() ?若存在,求出实数
?若存在,求出实数![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某校组织的“共筑中国梦”竞赛活动中,甲、乙两班各有6名选手参赛,在第一轮笔试环节中,评委将他们的笔试成绩作为样本数据,绘制成如图所示的茎叶图,为了增加结果的神秘感,主持人故意没有给出甲、乙两班最后一位选手的成绩,只是告知大家,如果某位选手的成绩高于90分(不含90分),则直接“晋级”.
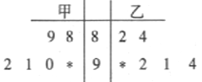
(1)求乙班总分超过甲班的概率;
(2)主持人最后宣布:甲班第六位选手的得分是90分,乙班第六位选手的得分是97分,
①请你从平均分和方差的角度来分析两个班的选手的情况;
②主持人从甲乙两班所有选手成绩中分别随机抽取2个,记抽取到“晋级”选手的总人数为![]() ,求
,求![]() 的分
的分
布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省电视台为了解该省卫视一档成语类节目的收视情况,抽查东西两部各个城市,得到观看该节目的人数(单位:千人),如茎叶图所示,其中一个数字被污损.
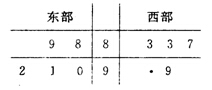
(1)求东部各城市观看该节目观众平均人数超过西部各城市观看该节目观众平均人数的概率;
(2)随着节目的播出,极大激发了观众对成语知识学习积累的热情,从中获益匪浅.现从观看该节目的观众中随机统计了位观众的周均学习成语知识的时间(单位:小时)与年龄(单位:岁),并制作了对照表(如下表所示),
年龄x(岁) | ||||
周均学习成语知识时间y(小时) |
由表中数据,试求线性回归方程,并预测年龄为岁观众周均学习成语知识时间.
参考公式: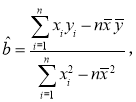 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() 满足
满足 ![]() (其中
(其中 ![]() ,
, ![]() ).
).
(1)求 ![]() 的表达式;
的表达式;
(2)对于函数 ![]() ,当
,当 ![]() 时,
时, ![]() ,求实数
,求实数 ![]() 的取值范围.
的取值范围.
(3)当 ![]() 时,
时, ![]() 的值为负数,求
的值为负数,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com