
ΓΨΧβΡΩΓΩΓΑΑ―ΡψΒΡ–ΡΈ“ΒΡ–Ρ¥°“Μ¥°Θ§¥°“Μ÷ξ–“‘Υ≤ί¥°“ΜΗωΆ§–Ρ‘≤Γ≠Γ±“ΜΈΜ ΐ―ßάœ Π“Μ’βΨδΗη¥ ΈΣΝιΗ–ΙΙ‘λΝΥ“ΜΒάΟϊΈΣΓΕΑ°2017ΓΖΒΡΧβΡΩΘ§«κΡψΫβ¥π¥ΥΧβΘΚ…ηOΈΣΉχ±ξ‘≠ΒψΘ§÷±œΏl”κ‘≤C1ΘΚx2+y2=1œύ«–«“”κ‘≤C2ΘΚx2+y2=r2Θ®rΘΨ1Θ©œύΫΜ”ΎAΓΔBΝΫ≤ΜΆ§ΒψΘ§“―÷Σ![]() EΘ®x1Θ§y1Θ©ΓΔFΘ®x2Θ§y2Θ©Ζ÷±π «‘≤C1ΓΔ‘≤C2…œΒΡΒψΘ°
EΘ®x1Θ§y1Θ©ΓΔFΘ®x2Θ§y2Θ©Ζ÷±π «‘≤C1ΓΔ‘≤C2…œΒΡΒψΘ°
Θ®1Θ©«σrΒΡ÷ΒΘΜ
Θ®2Θ©«σΓςOEFΟφΜΐΒΡΉν¥σ÷ΒΘΜ
Θ®3Θ©»τΓςOEFΒΡΆβΫ”‘≤‘≤–ΡP‘Ύ‘≤C1…œΘ§“―÷ΣΒψDΘ®3Θ§0Θ©Θ§«σ|DE|2+|DF|2ΒΡ»Γ÷ΒΖΕΈßΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©r=2ΘΜΘ®2Θ©1ΘΜΘ®3Θ©[23©¹6![]() Θ§23+6
Θ§23+6![]() ].
].
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚΘ®1Θ©÷±œΏl”κ‘≤C1ΘΚx2+y2=1œύ«–ΒΡ«–ΒψP «œ“ABΒΡ÷–ΒψΘ§άϊ”ΟΙ¥Ι…Ε®άμΘ§Ω…ΒΟrΒΡ÷ΒΘΜΘ®2Θ©Β±OEΓΆOF ±Θ§ΓςOEFΟφΜΐ»ΓΉν¥σ÷ΒΘΜΘ®3Θ©ΓςOEFΒΡΆβΫ”‘≤‘≤–ΡP‘Ύ‘≤C1…œΘ§‘ρΓςOEFΒΡΆβΫ”‘≤”κC2ΡΎ«–Θ§«“ΓœEOP=60ΓψΘ§≤ΜΖΝΝνPΘ®cosΠΝΘ§sinΠΝΘ©Θ§‘ρFΘ®2cosΠΝΘ§2sinΠΝΘ©Θ§EΘ®cosΘ®ΠΝ+60ΓψΘ©Θ§sinΘ®ΠΝ+60ΓψΘ©Θ©Θ§ΫαΚœΒψDΘ®3Θ§0Θ©Θ§άϊ”ΟœρΝΩΖ®ΫαΚœ»ΐΫ«Κ· ΐΘ§«σ≥ω|DE|2+|DF|2ΒΡ»Γ÷ΒΖΕΈßΘ°
‘ΧβΫβΈωΘΚ
Θ®1Θ©»γΆΦΥυ ΨΘ§÷±œΏl”κ‘≤C1ΘΚx2+y2=1œύ«–ΒΡ«–ΒψP «œ“ABΒΡ÷–ΒψΘ§
«“OPΓΆABΘ§AB=2AP=2![]() Θ§ΫβΒΟr=2ΘΜ
Θ§ΫβΒΟr=2ΘΜ
Θ®2Θ©ΓςOEFΒΡΟφΜΐS=![]() |OE|ΓΝ|OF|sinΓœEOFΘ§
|OE|ΓΝ|OF|sinΓœEOFΘ§
Ι Β±OEΓΆOF ±Θ§ΓςOEFΟφΜΐΒΡΉν¥σ÷ΒΈΣΘΚS=![]() |OE|ΓΝ|OF|=
|OE|ΓΝ|OF|=![]() ΓΝ1ΓΝ2=1ΘΜ
ΓΝ1ΓΝ2=1ΘΜ
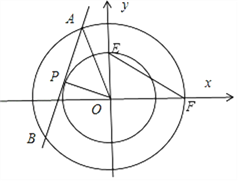
Θ®3Θ©ΓςOEFΒΡΆβΫ”‘≤‘≤–ΡP‘Ύ‘≤C1…œΘ§
Φ¥PE=PF=PO=1Θ§
‘ρΓςOEFΒΡΆβΫ”‘≤”κC2ΡΎ«–Θ§«“ΓœEOP=60ΓψΘ§
≤ΜΖΝΝνPΘ®cosΠΝΘ§sinΠΝΘ©Θ§‘ρFΘ®2cosΠΝΘ§2sinΠΝΘ©Θ§EΘ®cosΘ®ΠΝ+60ΓψΘ©Θ§sinΘ®ΠΝ+60ΓψΘ©Θ©Θ§
ΓΏΒψDΘ®3Θ§0Θ©Θ§
Γύ![]() =Θ®cosΘ®ΠΝ+60ΓψΘ©©¹3Θ§sinΘ®ΠΝ+60ΓψΘ©Θ©Θ§
=Θ®cosΘ®ΠΝ+60ΓψΘ©©¹3Θ§sinΘ®ΠΝ+60ΓψΘ©Θ©Θ§![]() =Θ®2cosΠΝ©¹3Θ§2sinΠΝΘ©Θ§
=Θ®2cosΠΝ©¹3Θ§2sinΠΝΘ©Θ§
|DE|2+|DF|2=[cosΘ®ΠΝ+60ΓψΘ©©¹3]2+sin2Θ®ΠΝ+60ΓψΘ©+Θ®2cosΠΝ©¹3Θ©2+Θ®2sinΠΝΘ©2
=23©¹15cosΠΝ+3![]() sinΠΝ
sinΠΝ
=6![]() sinΘ®ΠΝ©¹Π’Θ©+23Θ§Τδ÷–tanΠ’=
sinΘ®ΠΝ©¹Π’Θ©+23Θ§Τδ÷–tanΠ’=![]() Θ§
Θ§
Ι |DE|2+|DF|2ΒΡ»Γ÷ΒΖΕΈßΈΣ[23©¹6![]() Θ§23+6
Θ§23+6![]() ]
]


 ―ßΝΖΩλ≥ΒΒάΩλά÷ΦΌΤΎΚ°ΦΌΉς“ΒœΒΝ–¥πΑΗ
―ßΝΖΩλ≥ΒΒάΩλά÷ΦΌΤΎΚ°ΦΌΉς“ΒœΒΝ–¥πΑΗ –¬ΥΦΈ§Κ°ΦΌΉς“ΒœΒΝ–¥πΑΗ
–¬ΥΦΈ§Κ°ΦΌΉς“ΒœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ»ΐάβΉΕPΘ≠ABC÷–Θ§PAΓΆABΘ§PAΓΆBCΘ§ABΓΆBCΘ§PAΘΫABΘΫBCΘΫ2Θ§DΈΣœΏΕΈACΒΡ÷–ΒψΘ§EΈΣœΏΕΈPC…œ“ΜΒψ.

(1)«σ÷ΛΘΚPAΓΆBDΘΜ
(2)«σ÷ΛΘΚΤΫΟφBDEΓΆΤΫΟφPACΘΜ
(3)Β±PAΓΈΤΫΟφBDE ±Θ§«σ»ΐάβΉΕEΘ≠BCDΒΡΧεΜΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() Θ°
Θ°
Θ®1Θ©Β±![]() ±Θ§«σΚ· ΐ
±Θ§«σΚ· ΐ![]() ‘ΎΒψ
‘ΎΒψ![]() ¥ΠΒΡ«–œΏΖΫ≥ΧΘΜ
¥ΠΒΡ«–œΏΖΫ≥ΧΘΜ
Θ®2Θ©«σΚ· ΐ![]() ΒΡΦΪ÷ΒΘΜ
ΒΡΦΪ÷ΒΘΜ
Θ®3Θ©»τΚ· ΐ![]() ‘Ύ«χΦδ
‘Ύ«χΦδ![]() …œ «‘ωΚ· ΐΘ§ ‘»ΖΕ®
…œ «‘ωΚ· ΐΘ§ ‘»ΖΕ®![]() ΒΡ»Γ÷ΒΖΕΈßΘ°
ΒΡ»Γ÷ΒΖΕΈßΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() ΘΜΘ®2Θ©Β±
ΘΜΘ®2Θ©Β±![]() ±Θ§
±Θ§ ![]() Κψ≥…ΝΔΘ§
Κψ≥…ΝΔΘ§ ![]() ≤Μ¥φ‘ΎΦΪ÷ΒΘ°Β±
≤Μ¥φ‘ΎΦΪ÷ΒΘ°Β±![]() ±Θ§
±Θ§
![]() ”–ΦΪ–Γ÷Β
”–ΦΪ–Γ÷Β![]() ΈόΦΪ¥σ÷ΒΘ°Θ®3Θ©
ΈόΦΪ¥σ÷ΒΘ°Θ®3Θ©![]() Θ°
Θ°
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚ
Θ®1Θ©Β±![]() ±Θ§«σΒΟ
±Θ§«σΒΟ![]() Θ§ΒΟΒΫ
Θ§ΒΟΒΫ![]() ΒΡ÷ΒΘ§Φ¥Ω…«σΫβ«–œΏΖΫ≥Χ.
ΒΡ÷ΒΘ§Φ¥Ω…«σΫβ«–œΏΖΫ≥Χ.
Θ®2Θ©”…Ε®“ε”ρΈΣ![]() Θ§«σΒΟ
Θ§«σΒΟ![]() Θ§Ζ÷
Θ§Ζ÷![]() ΚΆ
ΚΆ![]() ±Ζ÷άύΧ÷¬έΒΟ≥ωΚ· ΐΒΡΒΞΒς«χΦδΘ§Φ¥Ω…«σΫβΚ· ΐΒΡΦΪ÷ΒΘ°
±Ζ÷άύΧ÷¬έΒΟ≥ωΚ· ΐΒΡΒΞΒς«χΦδΘ§Φ¥Ω…«σΫβΚ· ΐΒΡΦΪ÷ΒΘ°
Θ®3Θ©ΗυΨίΧβ“β![]() ‘Ύ
‘Ύ![]() …œΒί‘ωΘ§ΒΟ
…œΒί‘ωΘ§ΒΟ![]() Ε‘
Ε‘![]() Κψ≥…ΝΔΘ§ΫχΕχ«σΫβ Β ΐ
Κψ≥…ΝΔΘ§ΫχΕχ«σΫβ Β ΐ![]() ΒΡ»Γ÷ΒΖΕΈßΘ°
ΒΡ»Γ÷ΒΖΕΈßΘ°
‘ΧβΫβΈωΘΚ
Θ®1Θ©Β±![]() ±Θ§
±Θ§ ![]() Θ§
Θ§ ![]() Θ§
Θ§
![]() Θ§”÷
Θ§”÷![]() Θ§Γύ«–œΏΖΫ≥ΧΈΣ
Θ§Γύ«–œΏΖΫ≥ΧΈΣ![]() .
.
Θ®2Θ©Ε®“ε”ρΈΣ![]() Θ§
Θ§ ![]() Θ§Β±
Θ§Β±![]() ±Θ§
±Θ§ ![]() Κψ≥…ΝΔΘ§
Κψ≥…ΝΔΘ§ ![]() ≤Μ¥φ‘ΎΦΪ÷ΒΘ°
≤Μ¥φ‘ΎΦΪ÷ΒΘ°
Β±![]() ±Θ§Νν
±Θ§Νν![]() Θ§ΒΟ
Θ§ΒΟ![]() Θ§Β±
Θ§Β±![]() ±Θ§
±Θ§ ![]() ΘΜΒ±
ΘΜΒ±![]() ±Θ§
±Θ§ ![]() Θ§
Θ§
Υυ“‘Β±![]() ±Θ§
±Θ§ ![]() ”–ΦΪ–Γ÷Β
”–ΦΪ–Γ÷Β![]() ΈόΦΪ¥σ÷ΒΘ°
ΈόΦΪ¥σ÷ΒΘ°
Θ®3Θ©ΓΏ![]() ‘Ύ
‘Ύ![]() …œΒί‘ωΘ§Γύ
…œΒί‘ωΘ§Γύ![]() Ε‘
Ε‘![]() Κψ≥…ΝΔΘ§Φ¥
Κψ≥…ΝΔΘ§Φ¥![]() Κψ≥…ΝΔΘ§Γύ
Κψ≥…ΝΔΘ§Γύ![]() Θ°
Θ°
ΒψΨΠΘΚΒΦ ΐ «―–ΨΩΚ· ΐΒΡΒΞΒς–‘ΓΔΦΪ÷Β(Ήν÷Β)Ήν”––ßΒΡΙΛΨΏΘ§ΕχΚ· ΐ «ΗΏ÷– ΐ―ß÷–÷Ί“ΣΒΡ÷Σ ΕΒψΘ§Υυ“‘‘ΎάζΫλΗΏΩΦ÷–Θ§Ε‘ΒΦ ΐΒΡ”Π”ΟΒΡΩΦ≤ιΕΦΖ«≥ΘΆΜ≥ω Θ§±ΨΉ®Χβ‘ΎΗΏΩΦ÷–ΒΡΟϋΧβΖΫœρΦΑΟϋΧβΫ«Ε» ¥”ΗΏΩΦά¥Ω¥Θ§Ε‘ΒΦ ΐΒΡ”Π”ΟΒΡΩΦ≤ι÷ς“Σ¥”“‘œ¬ΦΗΗωΫ«Ε»Ϋχ––ΘΚ (1)ΩΦ≤ιΒΦ ΐΒΡΦΗΚΈ“β“εΘ§ΆυΆυ”κΫβΈωΦΗΚΈΓΔΈΔΜΐΖ÷œύΝΣœΒΘ° (2)άϊ”ΟΒΦ ΐ«σΚ· ΐΒΡΒΞΒς«χΦδΘ§≈–ΕœΒΞΒς–‘ΘΜ“―÷ΣΒΞΒς–‘Θ§«σ≤Έ ΐΘ° (3)ΩΦ≤ι ΐ–ΈΫαΚœΥΦœκΒΡ”Π”ΟΘ°
ΓΨΧβ–ΆΓΩΫβ¥πΧβ
ΓΨΫα χΓΩ
22
ΓΨΧβΡΩΓΩ“―÷Σ‘≤![]() ΘΚ
ΘΚ ![]() ΚΆΒψ
ΚΆΒψ![]() Θ§
Θ§ ![]() «‘≤
«‘≤![]() …œ»Έ“β“ΜΒψΘ§œΏΕΈ
…œ»Έ“β“ΜΒψΘ§œΏΕΈ![]() ΒΡ¥Ι÷±ΤΫΖ÷œΏΚΆ
ΒΡ¥Ι÷±ΤΫΖ÷œΏΚΆ![]() œύΫΜ”ΎΒψ
œύΫΜ”ΎΒψ![]() Θ§
Θ§ ![]() ΒΡΙλΦΘΈΣ«ζœΏ
ΒΡΙλΦΘΈΣ«ζœΏ![]() Θ°
Θ°
Θ®1Θ©«σ«ζœΏ![]() ΒΡΖΫ≥ΧΘΜ
ΒΡΖΫ≥ΧΘΜ
Θ®2Θ©Βψ![]() ««ζœΏ
««ζœΏ![]() ”κ
”κ![]() ÷α’ΐΑκ÷αΒΡΫΜΒψΘ§÷±œΏ
÷α’ΐΑκ÷αΒΡΫΜΒψΘ§÷±œΏ![]() ΫΜ
ΫΜ![]() ”Ύ
”Ύ![]() ΓΔ
ΓΔ![]() ΝΫΒψΘ§÷±œΏ
ΝΫΒψΘ§÷±œΏ![]() Θ§
Θ§ ![]() ΒΡ–±¬ Ζ÷±π «
ΒΡ–±¬ Ζ÷±π «![]() Θ§
Θ§ ![]() Θ§»τ
Θ§»τ![]() Θ§«σΘΚΔΌ
Θ§«σΘΚΔΌ![]() ΒΡ÷ΒΘΜΔΎ
ΒΡ÷ΒΘΜΔΎ![]() ΟφΜΐΒΡΉν¥σ÷ΒΘ°
ΟφΜΐΒΡΉν¥σ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘Ύ÷±Ϋ«Ήχ±ξœΒxOy÷–Θ§«ζœΏ ![]() Θ§«ζœΏC2ΒΡ≤Έ ΐΖΫ≥ΧΈΣΘΚ
Θ§«ζœΏC2ΒΡ≤Έ ΐΖΫ≥ΧΈΣΘΚ ![]() Θ§Θ®Π»ΈΣ≤Έ ΐΘ©Θ§“‘OΈΣΦΪΒψΘ§x÷αΒΡ’ΐΑκ÷αΈΣΦΪ÷αΒΡΦΪΉχ±ξœΒΘ°
Θ§Θ®Π»ΈΣ≤Έ ΐΘ©Θ§“‘OΈΣΦΪΒψΘ§x÷αΒΡ’ΐΑκ÷αΈΣΦΪ÷αΒΡΦΪΉχ±ξœΒΘ°
Θ®1Θ©«σC1 Θ§ C2ΒΡΦΪΉχ±ξΖΫ≥ΧΘΜ
Θ®2Θ©…δœΏ ![]() ”κC1ΒΡ“λ”Ύ‘≠ΒψΒΡΫΜΒψΈΣAΘ§”κC2ΒΡΫΜΒψΈΣBΘ§«σ|AB|Θ°
”κC1ΒΡ“λ”Ύ‘≠ΒψΒΡΫΜΒψΈΣAΘ§”κC2ΒΡΫΜΒψΈΣBΘ§«σ|AB|Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§άβ≥ΛΈΣ2ΒΡ’ΐΖΫΧεABCD-A1B1C1D1÷–Θ§EΓΔFΖ÷±π «DD1ΓΔDBΒΡ÷–ΒψΘ§«σ÷ΛΘΚ
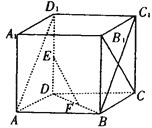
Θ®1Θ©EFΓΈΤΫΟφABC1D1ΘΜ
Θ®2Θ©EFΓΆB1C
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() .
.
Θ®ΔώΘ©≈–Εœ![]() ΒΡΒΞΒς–‘ΘΜ
ΒΡΒΞΒς–‘ΘΜ
Θ®ΔρΘ©»τ![]() ‘Ύ
‘Ύ![]() …œΒΡΉν–Γ÷ΒΈΣ2Θ§«σ
…œΒΡΉν–Γ÷ΒΈΣ2Θ§«σ![]() ΒΡ÷Β.
ΒΡ÷Β.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈΣœλ”ΠΒ≥÷–―κΓΑΖωΤΕΙΞΦαΓ±ΒΡΚ≈’ΌΘ§Ρ≥ΒΞΈΜ÷ΗΒΦ“ΜΤΕάß¥εΆ®Ιΐ÷÷÷≤ΉœΗ μά¥ΧαΗΏΨ≠ΦΟ ’»κ.ΉœΗ μΕ‘ΜΖΨ≥Έ¬Ε»“Σ«σΫœΗΏΘ§ΗυΨί“‘ΆυΒΡΨ≠―ιΘ§ΥφΉ≈Έ¬Ε»ΒΡ…ΐΗΏΘ§ΤδΥάΆω÷ξ ΐ≥…‘ω≥ΛΒΡ«ς Τ.œ¬±μΗχ≥ωΝΥ2018Ρξ÷÷÷≤ΒΡ“Μ≈ζ ‘―ιΉœΗ μ‘Ύ≤ΜΆ§Έ¬Ε» ±6ΉιΥάΆωΒΡ÷ξ ΐΘΚ
Έ¬Ε» | 21 | 23 | 24 | 27 | 29 | 32 |
ΥάΆω ΐ | 6 | 11 | 20 | 27 | 57 | 77 |
Ψ≠ΦΤΥψΘΚ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() .
.
Τδ÷–![]() Ζ÷±πΈΣ ‘―ι ΐΨί÷–ΒΡΈ¬Ε»ΚΆΥάΆω÷ξ ΐΘ§
Ζ÷±πΈΣ ‘―ι ΐΨί÷–ΒΡΈ¬Ε»ΚΆΥάΆω÷ξ ΐΘ§![]() Θ°
Θ°
(1)![]() ”κ
”κ![]() «Ζώ”–Ϋœ«ΩΒΡœΏ–‘œύΙΊ–‘? «κΦΤΥψœύΙΊœΒ ΐ
«Ζώ”–Ϋœ«ΩΒΡœΏ–‘œύΙΊ–‘? «κΦΤΥψœύΙΊœΒ ΐ![]() (ΨΪ»ΖΒΫ
(ΨΪ»ΖΒΫ![]() )ΥΒΟς.
)ΥΒΟς.
(2)≤Δ«σ![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ΒΡΜΊΙιΖΫ≥Χ
ΒΡΜΊΙιΖΫ≥Χ![]() (
(![]() ΚΆ
ΚΆ![]() ΕΦΨΪ»ΖΒΫ
ΕΦΨΪ»ΖΒΫ![]() )ΘΜ
)ΘΜ
(3)”Ο(2)÷–ΒΡœΏ–‘ΜΊΙιΡΘ–Ά‘Λ≤βΈ¬Ε»ΈΣ![]() ±ΗΟ≈ζΉœΗ μΥάΆω÷ξ ΐ(ΫαΙϊ»Γ’ϊ ΐ)Θ°
±ΗΟ≈ζΉœΗ μΥάΆω÷ξ ΐ(ΫαΙϊ»Γ’ϊ ΐ)Θ°
ΗΫΘΚΕ‘”Ύ“ΜΉι ΐΨί![]() Θ§
Θ§![]() Θ§Γ≠Γ≠Θ§
Θ§Γ≠Γ≠Θ§![]() Θ§
Θ§
ΔΌœΏ–‘œύΙΊœΒ ΐ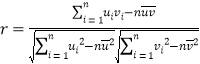 Θ§Ά®≥Θ«ιΩωœ¬Β±
Θ§Ά®≥Θ«ιΩωœ¬Β±![]() ¥σ”Ύ0.8 ±Θ§»œΈΣΝΫ
¥σ”Ύ0.8 ±Θ§»œΈΣΝΫ
Ηω±δΝΩ”–Κή«ΩΒΡœΏ–‘œύΙΊ–‘Θ°
ΔΎΤδΜΊΙι÷±œΏ![]() ΒΡ–±¬ ΚΆΫΊΨύΒΡΉν–ΓΕΰ≥ΥΙάΦΤΖ÷±πΈΣΘΚ
ΒΡ–±¬ ΚΆΫΊΨύΒΡΉν–ΓΕΰ≥ΥΙάΦΤΖ÷±πΈΣΘΚ
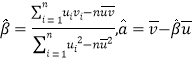 ΘΜ
ΘΜ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘ΎΤΫ÷±Ϋ«Ήχ±ξœΒ![]() ÷–Θ§“―÷ΣΒψ
÷–Θ§“―÷ΣΒψ![]() Θ§
Θ§![]()
Θ®1Θ©‘Ύ![]() ÷αΒΡ’ΐΑκ÷α…œ«σ“ΜΒψ
÷αΒΡ’ΐΑκ÷α…œ«σ“ΜΒψ![]() Θ§ ΙΒΟ“‘
Θ§ ΙΒΟ“‘![]() ΈΣ÷±ΨΕΒΡ‘≤Ιΐ
ΈΣ÷±ΨΕΒΡ‘≤Ιΐ![]() ΒψΘ§≤Δ«σΗΟ‘≤ΒΡΖΫ≥Χ;
ΒψΘ§≤Δ«σΗΟ‘≤ΒΡΖΫ≥Χ;
Θ®2Θ©‘ΎΘ®1Θ©ΒΡΧθΦΰœ¬Θ§Βψ![]() ‘ΎœΏΕΈ
‘ΎœΏΕΈ![]() ΡΎΘ§«“
ΡΎΘ§«“![]() ΤΫΖ÷
ΤΫΖ÷![]() Θ§ ‘«σ
Θ§ ‘«σ![]() ΒψΒΡΉχ±ξ.
ΒψΒΡΉχ±ξ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com