已知函数f (x)=loga x (a>0且a≠1),若数列:2,f (a1),f (a2),…,f (an),2n+4 (n∈N﹡)为等差数列.
(1)求数列{an}的通项公式an;
(2)若a=2,bn=an•f (an),求数列{bn}前n项和Sn;
(3)在(2)的条件下对任意的n∈N﹡,都有bn>f -1(t),求实数t的取值范围.
解:(1)由题意2n+4=2+(n+2-1)d求得:d=2,
所以f (a
n)=2+(n+1-1)•2=2n+2,求得:a
n=a
2n+2.(4分)
(2)b
n=a
n•f (a
n)=(2n+2)a
2n+2=(n+1)•a
2n+3S
n=2•2
5+3•2
7+4•2
9+…+(n+1)•2
2n+3,
4S
n=2•2
7+3•2
7+4•2
11+…+(n+1)•2
2(n+1)+3,
错位相减得:
S
n=
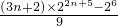
(8分)
(3)∵
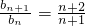
•4>1,
∴{ b
n }为递增数列.b
n中的最小项为:b
1=2•2
5=2
6,f
-1(t)=2
t,
对任意的n∈N
﹡,都有b
n>f
-1(t),可得2
6>2
t,
∴t<6.(14分)
分析:(1)由数列:2,f (a
1),f (a
2),…,f (a
n),2n+4 (n∈N
﹡)为等差数列.可得出2n+4=2+(n+2-1)d求得:d=2,由此可求出f (a
n),进而即可求出数列{a
n}的通项公式a
n;
(2)若a=2,b
n=a
n•f (a
n),可先解出b
n=a
n•f (a
n)=(2n+2)a
2n+2=(n+1)•a
2n+3,由此通项公式的形式知,可用错位相减法求得数列{b
n}前n项和S
n;
(3)在(2)的条件下对任意的n∈N
﹡,都有b
n>f
-1(t),故可由
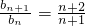
•4>1,得出数列是一个递增的数列,由此得出b
n的最小值,令最小值大于f
-1(t),解此不等式即可得出实数t的取值范围
点评:本师考查等差数列的性质与等比数列的性质,数列单调性,解不等式,错位相减法求和,综合性强,解题的关键是将题设中的问题正确转化,熟练运用等差等比数列的性质及错位相减法是解题的重点.

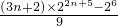 (8分)
(8分)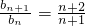 •4>1,
•4>1,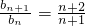 •4>1,得出数列是一个递增的数列,由此得出bn的最小值,令最小值大于f -1(t),解此不等式即可得出实数t的取值范围
•4>1,得出数列是一个递增的数列,由此得出bn的最小值,令最小值大于f -1(t),解此不等式即可得出实数t的取值范围
