
【题目】伴随着智能手机的深入普及,支付形式日渐多样化,打破了传统支付的局限性和壁垒,有研究表明手机支付的使用比例与人的年龄存在一定的关系,某调研机构随机抽取了50人,对他们一个月内使用手机支付的情况进行了统计,如下表:

(1)若以“年龄55岁为分界点”,由以上统计数据完成下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为“使用手机支付”与人的年龄有关;
的把握认为“使用手机支付”与人的年龄有关;

(2)若从年龄在![]() ,
,![]() 内的被调查人中各随机选取2人进行追踪调查,记选中的4人中“使用手机支付”的人数为
内的被调查人中各随机选取2人进行追踪调查,记选中的4人中“使用手机支付”的人数为![]() .
.
①求随机变量![]() 的分布列;
的分布列;
②求随机变量![]() 的数学期望.
的数学期望.
参考数据如下:
| 0.05 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
参考格式:![]() ,其中
,其中![]()
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:
【题目】已知定义在R上的奇函数f(x),且对任意实数x1,x2,x1≠x2时,都有(f(x1)﹣f(x2))(x1﹣x2)<0.若存在实数x∈[﹣3,3],使得不等式f(a﹣x)+f(a2﹣x)>0成立,则实数a的取值范围是( )
A.(﹣3,2)B.[﹣3,2]C.(﹣2,1)D.[﹣2,1]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某老小区建成时间较早,没有集中供暖,随着人们生活水平的日益提高热力公司决定在此小区加装暖气该小区的物业公司统计了近五年(截止2018年年底)小区居民有意向加装暖气的户数,得到如下数据
年份编号x | 1 | 2 | 3 | 4 | 5 |
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
加装户数y | 34 | 95 | 124 | 181 | 216 |
(Ⅰ)若有意向加装暖气的户数y与年份编号x满足线性相关关系求y与x的线性回归方程并预测截至2019年年底,该小区有多少户居民有意向加装暖气;
(Ⅱ)2018年年底郑州市民生工程决定对老旧小区加装暖气进行补贴,该小区分到120个名额物业公司决定在2019年度采用网络竞拍的方式分配名额,竞拍方案如下:①截至2018年年底已登记在册的居民拥有竞拍资格;②每户至多申请一个名额,由户主在竞拍网站上提出申请并给出每平方米的心理期望报价;③根据物价部门的规定,每平方米的初装价格不得超过300元;④申请阶段截止后,将所有申请居民的报价自高到低排列,排在前120位的业主以其报价成交;⑤若最后出现并列的报价,则认为申请时问在前的居民得到名额,为预测本次竞拍的成交最低价,物业公司随机抽取了有竞拍资格的50位居民进行调查统计了他们的拟报竞价,得到如图所示的频率分布直方图:

(1)求所抽取的居民中拟报竞价不低于成本价180元的人数;
(2)如果所有符合条件的居民均参与竞拍,请你利用样本估计总体的思想预测至少需要报价多少元才能获得名额(结果取整数)
参考公式对于一组数据(x1,y1),(x2,y2),(x3,y3),…(xn,yn),其回归直线![]() 的斜率和截距的最小二乘估计分别为,
的斜率和截距的最小二乘估计分别为,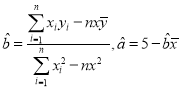
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,过点
,过点![]() 作与
作与![]() 轴平行的直线
轴平行的直线![]() ,点
,点![]() 为动点
为动点![]() 在直线
在直线![]() 上的投影,且满足
上的投影,且满足![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)已知点![]() 为曲线
为曲线![]() 上的一点,且曲线
上的一点,且曲线![]() 在点
在点![]() 处的切线为
处的切线为![]() ,若
,若![]() 与直线
与直线![]() 相交于点
相交于点![]() ,试探究在
,试探究在![]() 轴上是否存在点
轴上是否存在点![]() ,使得以
,使得以![]() 为直径的圆恒过点
为直径的圆恒过点![]() ?若存在,求出点
?若存在,求出点![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某玩具厂生产出一种新型儿童泡沫玩具飞机,为更精确的确定最终售价,该厂采用了多种价格对该玩具飞机进行了试销,某销售点的销售情况如下表:
单价 | 8 | 9 | 10 | 11 | 12 |
销量 | 40 | 36 | 30 | 24 | 20 |
从散点图可以看出,这些点大致分布在一条直线的附近,变量![]() ,
,![]() 有较强的线性相关性.
有较强的线性相关性.
(1)求销量![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)若每架该玩具飞机的成本价为5元,利用(1)的结果,预测每架该玩具飞机的定价为多少元时,总利润最大.(结果保留一位小数)
(附: ,
,![]() ,
,![]() ,
,![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某客户准备在家中安装一套净水系统,该系统为三级过滤,使用寿命为十年.如图所示,两个一级过滤器采用并联安装,二级过滤器与三级过滤器为串联安装。

其中每一级过滤都由核心部件滤芯来实现。在使用过程中,一级滤芯和二级滤芯都需要不定期更换(每个滤芯是否需要更换相互独立),三级滤芯无需更换,若客户在安装净水系统的同时购买滤芯,则一级滤芯每个![]() 元,二级滤芯每个
元,二级滤芯每个![]() 元.若客户在使用过程中单独购买滤芯,则一级滤芯每个
元.若客户在使用过程中单独购买滤芯,则一级滤芯每个![]() 元,二级滤芯每个
元,二级滤芯每个![]() 元。现需决策安装净水系统的同时购滤芯的数量,为此参考了根据
元。现需决策安装净水系统的同时购滤芯的数量,为此参考了根据![]() 套该款净水系统在十年使用期内更换滤芯的相关数据制成的图表,其中图是根据
套该款净水系统在十年使用期内更换滤芯的相关数据制成的图表,其中图是根据![]() 个一级过滤器更换的滤芯个数制成的柱状图,表是根据
个一级过滤器更换的滤芯个数制成的柱状图,表是根据![]() 个二级过滤器更换的滤芯个数制成的频数分布表.
个二级过滤器更换的滤芯个数制成的频数分布表.

二级滤芯更换频数分布表
二级滤芯更换的个数 |
|
|
频数 |
|
|
以![]() 个一级过滤器更换滤芯的频率代替
个一级过滤器更换滤芯的频率代替![]() 个一级过滤器更换滤芯发生的概率,以
个一级过滤器更换滤芯发生的概率,以![]() 个二级过滤器更换滤芯的频率代替
个二级过滤器更换滤芯的频率代替![]() 个二级过滤器更换滤芯发生的概率.
个二级过滤器更换滤芯发生的概率.
(1)求一套净水系统在使用期内需要更换的各级滤芯总个数恰好为![]() 的概率;
的概率;
(2)记![]() 表示该客户的净水系统在使用期内需要更换的一级滤芯总数,求
表示该客户的净水系统在使用期内需要更换的一级滤芯总数,求![]() 的分布列及数学期望;
的分布列及数学期望;
(3)记![]() ,
,![]() 分别表示该客户在安装净水系统的同时购买的一级滤芯和二级滤芯的个数.若
分别表示该客户在安装净水系统的同时购买的一级滤芯和二级滤芯的个数.若![]() ,且
,且![]() ,以该客户的净水系统在使用期内购买各级滤芯所需总费用的期望值为决策依据,试确定
,以该客户的净水系统在使用期内购买各级滤芯所需总费用的期望值为决策依据,试确定![]() ,
,![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com