
【题目】我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年![]() 位居民每人的月均用水量(单位:吨),将数据按照
位居民每人的月均用水量(单位:吨),将数据按照![]() 分成
分成![]() 组,制成了如图所示的频率分布直方图.
组,制成了如图所示的频率分布直方图.
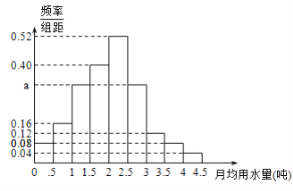
(1)求直方图中的![]() 值;
值;
(2)设该市有![]() 万居民,估计全市居民中月均用水量不低于
万居民,估计全市居民中月均用水量不低于![]() 吨的人数.说明理由;
吨的人数.说明理由;
(3)估计居民月均用水量的中位数.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直(其中
垂直(其中![]() 为自然对数的底数).
为自然对数的底数).
(1)求![]() 的解析式及单调递减区间;
的解析式及单调递减区间;
(2)是否存在常数![]() ,使得对于定义域内的任意
,使得对于定义域内的任意![]() ,
, ![]() 恒成立,若存在,求出
恒成立,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次测量中得到的A样本数据如下:82,84,84,86,86,86,88,88,88,88.若B样本数据恰好是A样本数据每个都加2后所得数据,则A,B两样本的下列数字特征对应相同的是( )
A. 众数 B. 平均数 C. 标准差 D. 中位数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等差数列{an}的公差不为零,首项a1=1,a2是a1和a5的等比中项,则数列的前10项之和是( )
A. 90 B. 100 C. 145 D. 190
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(1,0,2),B(1,-3,1),点M在z轴上且到A、B两点的距离相等,则点M的坐标为
A. (-3,0,0) B. (0,-3,0) C. (0,0,3) D. (0,0,-3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com