
【题目】炼钢是一个氧化降碳的过程,钢水含碳量的多少直接影响冶炼时间的长短,必须掌握钢水含碳量和冶炼时间的关系.如果已测得炉料溶化完毕时钢水的含碳量x与冶炼时间y(从炉料溶化完毕到出钢的时间)的一组数据,如表所示:
x(0.01%) | 104 | 180 | 190 | 177 | 147 | 134 | 150 | 191 | 204 | 121 |
y/min | 100 | 200 | 210 | 185 | 155 | 135 | 170 | 205 | 235 | 125 |
(1)y与x是否具有线性相关关系?
(2)如果y与x具有线性相关关系,求回归直线方程.
(3)预报当钢水含碳量为160个0.01%时,应冶炼多少分钟?
参考公式:r=![]()
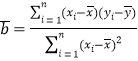 ,
,
线性回归方程![]()
【答案】(1) 见解析;(2)![]() =1.267x-30.47. (3)172分钟.
=1.267x-30.47. (3)172分钟.
【解析】试题分析:(1)根据题意列表并计算r≈0.9906>0.75,可得结论;
(2)利用(1)中所求的数据可以求得![]() ≈1.267,
≈1.267, ![]() =-30.47,可得所求的回归直线方程;
=-30.47,可得所求的回归直线方程;
(3)当x=160时,代入计算,可得结论.
试题解析:(1)根据题意列表并计算如表:
i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
xi | 104 | 180 | 190 | 177 | 147 | 134 | 150 | 191 | 204 | 121 |
yi | 100 | 200 | 210 | 185 | 155 | 135 | 170 | 205 | 235 | 125 |
x1yi | 10400 | 36000 | 39900 | 32745 | 22785 | 18090 | 25500 | 39155 | 47940 | 15125 |
| ||||||||||
于是r=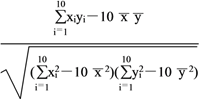 ≈0.9906>0.75.
≈0.9906>0.75.
∴y与x具有线性相关关系.
(2)利用(1)中所求的数据可以求得![]() ,
,![]() 的值为
的值为
![]() =
=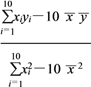 ≈1.267,
≈1.267,
![]() =
=![]() -
-![]()
![]() =-30.47,
=-30.47,
∴所求的回归直线方程![]() =1.267x-30.47.
=1.267x-30.47.
(3)当x=160时,
![]() =1.267×160-30.47≈172(min),
=1.267×160-30.47≈172(min),
即大约需要冶炼172分钟.


科目:高中数学 来源: 题型:
【题目】在某城市街道上一侧路边边缘![]() 某处安装路灯,路宽
某处安装路灯,路宽![]() 为
为![]() 米,灯杆
米,灯杆![]() 长4米,且与灯柱
长4米,且与灯柱![]() 成
成![]() 角,路灯采用可旋转灯口方向的锥形灯罩,灯罩轴线
角,路灯采用可旋转灯口方向的锥形灯罩,灯罩轴线![]() 与灯的边缘光线(如图
与灯的边缘光线(如图![]() ,
, ![]() )都成
)都成![]() 角,当灯罩轴线
角,当灯罩轴线![]() 与灯杆
与灯杆![]() 垂直时,灯罩轴线正好通过
垂直时,灯罩轴线正好通过![]() 的中点.
的中点.
(I)求灯柱![]() 的高
的高![]() 为多少米;
为多少米;
(II)设![]() ,且
,且![]() ,求灯所照射路面宽度
,求灯所照射路面宽度![]() 的最小值.
的最小值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,动点
,动点![]() 满足
满足![]() ,其中
,其中![]() 分别表示直线
分别表示直线![]() 的斜率,
的斜率,![]() 为常数,当
为常数,当![]() 时,点
时,点![]() 的轨迹为
的轨迹为![]() ;当
;当![]() 时,点
时,点![]() 的轨迹为
的轨迹为![]() .
.
(1)求![]() 的方程;
的方程;
(2)过点![]() 的直线与曲线
的直线与曲线![]() 顺次交于四点
顺次交于四点![]() ,且
,且![]() ,
,![]() ,是否存在这样的直线
,是否存在这样的直线![]() ,使得
,使得![]() 成等差数列?若存在,求出直线
成等差数列?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() ,侧面
,侧面![]() 是边长为2的正三角形,且平面
是边长为2的正三角形,且平面![]() 平面
平面![]() ,底面
,底面![]() 是
是![]() 的菱形,
的菱形, ![]() 为棱
为棱![]() 上的动点,且
上的动点,且![]() .
.
(Ⅰ)求证: ![]() ;
;
(Ⅱ)试确定![]() 的值,使得二面角
的值,使得二面角![]() 的平面角余弦值为
的平面角余弦值为![]() .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com