
【题目】数列![]() ,定义
,定义![]() 为数列
为数列![]() 的一阶差分数列,其中
的一阶差分数列,其中![]() .
.
(1)若![]() ,试判断
,试判断![]() 是否是等差数列,并说明理由;
是否是等差数列,并说明理由;
(2)若![]() ,
,![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(3)对(2)中的数列![]() ,是否存在等差数列
,是否存在等差数列![]() ,使得
,使得![]() 对一切
对一切![]() 都成立,若存在,求出数列
都成立,若存在,求出数列![]() 的通项公式;若不存在,请说明理由.
的通项公式;若不存在,请说明理由.
科目:高中数学 来源: 题型:
【题目】为庆祝新中国成立70周年,某市工会组织部分事业单位职工举行“迎国庆,广播操比赛”活动.现有200名职工参与了此项活动,将这200人按照年龄(单位:岁)分组:第一组[15,25),第二组[25,35),第三组[35,45),第四组[45,55),第五组[55,65],得到的频率分布直方图如图所示.记事件A为“从这200人中随机抽取一人,其年龄不低于35岁”,已知P(A)=0.75.
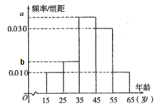
(1)求![]() 的值;
的值;
(2)在第二组、第四组中用分层抽样的方法抽取6人,再从这6人中随机抽取2人作为活动的负责人,求这2人恰好都在第四组中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知双曲线
中,已知双曲线![]() :
:![]() .
.
(1)设![]() 是
是![]() 的左焦点,
的左焦点,![]() 是
是![]() 右支上一点.若
右支上一点.若![]() ,求
,求![]() 点的坐标;
点的坐标;
(2)设斜率为1的直线![]() 交
交![]() 于
于![]() 、
、![]() 两点,若
两点,若![]() 与圆
与圆![]() 相切,求证:
相切,求证:![]() ;
;
(3)设椭圆![]() :
:![]() .若
.若![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的动点,且
上的动点,且![]() ,求证:
,求证:![]() 到直线
到直线![]() 的距离是定值.
的距离是定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在①![]() ;②
;②![]() 这两个条件中任选-一个,补充在下面问题中,然后解答补充完整的题.
这两个条件中任选-一个,补充在下面问题中,然后解答补充完整的题.

在![]() 中,角
中,角![]() 的对边分别为
的对边分别为![]() ,已知 ,
,已知 ,![]() .
.
(1)求![]() ;
;
(2)如图,![]() 为边
为边![]() 上一点,
上一点,![]() ,求
,求![]() 的面积
的面积
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若![]() 是一个集合,
是一个集合,![]() 是一个以
是一个以![]() 的某些子集为元素的集合,且满足:(1)
的某些子集为元素的集合,且满足:(1)![]() 属于
属于![]() ,
,![]() 属于
属于![]() ;(2)
;(2)![]() 中任意多个元素的并集属于
中任意多个元素的并集属于![]() ;(3)
;(3)![]() 中任意多个元素的交集属于
中任意多个元素的交集属于![]() ,则称
,则称![]() 是集合
是集合![]() 上的一个拓补.已知集合
上的一个拓补.已知集合![]() ,对于下面给出的四个集合
,对于下面给出的四个集合![]() :
:
①![]() ②
②![]()
③![]() ④
④![]()
其中是集合![]() 上的拓补的集合
上的拓补的集合![]() 的序号是______.(写出所有的拓补的集合
的序号是______.(写出所有的拓补的集合![]() 的序号)
的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com