
分析 (1)如图所示,由$\overrightarrow{BC}$=2$\overrightarrow{AD}$,且AB=CD=DA=2,可得B(-2,0),O(0,0),C(2,0),D(1,$\sqrt{3}$),O1(0,$\sqrt{3}$),A$(-1,\sqrt{3})$,M$(\frac{3}{2},\frac{\sqrt{3}}{2})$.令$\overrightarrow{BM}$=$m\overrightarrow{a}$+$n\overrightarrow{b}$,即可得出.
(2)如图所示,设$\overrightarrow{BP}=λ\overrightarrow{BA}$,则$\overrightarrow{OP}$=$(λ-2,\sqrt{3}λ)$.由于|$\overrightarrow{PQ}$|:|$\overrightarrow{QC}$|=1:2,可得$\overrightarrow{CQ}=\frac{2}{3}\overrightarrow{CP}$,于是$\overrightarrow{OQ}$=$\overrightarrow{OC}+\frac{2}{3}\overrightarrow{CP}$=$\frac{1}{3}\overrightarrow{OC}+\frac{2}{3}\overrightarrow{OP}$=$(\frac{2}{3}λ-\frac{2}{3},\frac{2\sqrt{3}}{3}λ)$.
由于B,Q,M三点共线,可得$\overrightarrow{OQ}=k\overrightarrow{OB}+(1-k)\overrightarrow{OM}$,可得$\left\{\begin{array}{l}{-2k+\frac{3}{2}(1-k)=\frac{2}{3}λ-\frac{2}{3}}\\{0+(1-k)×\frac{\sqrt{3}}{2}=\frac{2\sqrt{3}}{3}λ}\end{array}\right.$,即可得出.
解答 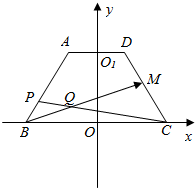 解:(1)如图所示,
解:(1)如图所示,
∵$\overrightarrow{BC}$=2$\overrightarrow{AD}$,且AB=CD=DA=2,
∴B(-2,0),O(0,0),C(2,0),D(1,$\sqrt{3}$),O1(0,$\sqrt{3}$),A$(-1,\sqrt{3})$,M$(\frac{3}{2},\frac{\sqrt{3}}{2})$.
$\overrightarrow{BM}$=$(\frac{7}{2},\frac{\sqrt{3}}{2})$.
$\overrightarrow{a}$=$\overrightarrow{AD}$=(2,0),$\overrightarrow{b}$=$\overrightarrow{BA}$=(1,$\sqrt{3}$).
令$\overrightarrow{BM}$=$m\overrightarrow{a}$+$n\overrightarrow{b}$,
则$(\frac{7}{2},\frac{\sqrt{3}}{2})$=m(2,0)+n(1,$\sqrt{3}$).
∴$\left\{\begin{array}{l}{2m+n=\frac{7}{2}}\\{\sqrt{3}n=\frac{\sqrt{3}}{2}}\end{array}\right.$,
解得n-$\frac{1}{2}$,m=$\frac{3}{2}$.
∴$\overrightarrow{BM}$=$\frac{3}{2}\overrightarrow{a}$+$\frac{1}{2}\overrightarrow{b}$.
(2)如图所示,设$\overrightarrow{BP}=λ\overrightarrow{BA}$,
则$\overrightarrow{OP}$=$(λ-2,\sqrt{3}λ)$.
∵|$\overrightarrow{PQ}$|:|$\overrightarrow{QC}$|=1:2,
∴$\overrightarrow{CQ}=\frac{2}{3}\overrightarrow{CP}$,
∴$\overrightarrow{OQ}$=$\overrightarrow{OC}+\frac{2}{3}\overrightarrow{CP}$=$\frac{1}{3}\overrightarrow{OC}+\frac{2}{3}\overrightarrow{OP}$=$(\frac{2}{3}λ-\frac{2}{3},\frac{2\sqrt{3}}{3}λ)$.
∵B,Q,M三点共线,
∴$\overrightarrow{OQ}=k\overrightarrow{OB}+(1-k)\overrightarrow{OM}$,
∴$\left\{\begin{array}{l}{-2k+\frac{3}{2}(1-k)=\frac{2}{3}λ-\frac{2}{3}}\\{0+(1-k)×\frac{\sqrt{3}}{2}=\frac{2\sqrt{3}}{3}λ}\end{array}\right.$,
解得λ=$\frac{1}{4}$,k=$\frac{2}{3}$.
∴|$\overrightarrow{AP}$|:|$\overrightarrow{PB}$|=3,
|$\overrightarrow{BQ}$|:|$\overrightarrow{QM}$|=$\frac{1}{2}$.
点评 本题考查了向量共线定理、向量的三角形法则、向量的坐标运算,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{36}$ | B. | $\frac{1}{6}$ | C. | $\frac{2}{15}$ | D. | $\frac{1}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{ON}$ | B. | $\overrightarrow{AM}$ | C. | $\overrightarrow{AN}$ | D. | 2$\overrightarrow{AN}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
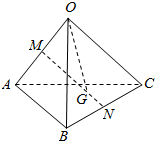 如图,在三棱锥O-ABC中,M,N分别是棱OA、CB的中点,点G在线段MN上,且MG=2GN,设$\overrightarrow{OA}$=a,$\overrightarrow{OB}$=b,$\overrightarrow{OC}$=c.
如图,在三棱锥O-ABC中,M,N分别是棱OA、CB的中点,点G在线段MN上,且MG=2GN,设$\overrightarrow{OA}$=a,$\overrightarrow{OB}$=b,$\overrightarrow{OC}$=c.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com