
”¾ĢāÄæ”æ½ā“šĢā
£Ø¢ń£©ŅŃÖŖ ![]() £¬ĘäÖŠai”ŹR£¬i=1£¬2£¬”10£®
£¬ĘäÖŠai”ŹR£¬i=1£¬2£¬”10£®
£Øi£©Ēóa0+a1+a2+”+a10£»
£Øii£©Ēóa7 £®
£Ø¢ņ£©2017Äź5ŌĀ£¬±±¾©ÕŁæŖ”°Ņ»“ųŅ»Ā·”±¹ś¼ŹŗĻ×÷øß·åĀŪĢ³£®×éĪÆ»į½«¼×”¢ŅŅ”¢±ū”¢¶””¢ĪģĪåĆūÖ¾ŌøÕß·ÖÅäµ½·Ņė”¢µ¼ÓĪ”¢ĄńŅĒ”¢Ė¾»śĖÄøö²»Ķ¬µÄøŚĪ»£¬ĆæøöøŚĪ»ÖĮÉŁÓŠŅ»ČĖ²Ī¼Ó£¬ĒŅĪåČĖ¾łÄÜŹ¤ČĪÕāĖÄøöøŚĪ»£®
£Øi£©ČōĆæČĖ²»×¼¼ęÖ°£¬Ōņ²»Ķ¬µÄ·ÖÅä·½°øÓŠ¼øÖÖ£æ
£Øii£©Čō¼×ŅŅ±»³éµ÷Č„±šµÄµŲ·½£¬Ź£ĻĀČżČĖŅŖĒóĆæČĖ±Ų¼ęĮ½Ö°£¬Ōņ²»Ķ¬µÄ·ÖÅä·½°øÓŠ¼øÖÖ£æ
”¾“š°ø”æ½ā£ŗ£Ø¢ń£©£Øi£©ŌŚ£Ø2x©1£©10=a0+a1£Øx©1£©+a2£Øx©1£©2+”+a10£Øx©1£©10ÖŠ£¬
Įīx=2æÉµĆ a0+a1+a2+”+a10=310£¬
£Øii£©Įīx©1=y£¬Ōņx=y+1£»
”ą£Ø1+2y£©10=a0+a1y+a2y2+”+a10y10£¬
”ąa7=C10727=15360£»
£Ø¢ņ£©£Øi£©ĆæøöøŚĪ»ÖĮÉŁÓŠŅ»ČĖ²Ī¼Ó£¬ĆæČĖ²»×¼¼ęÖ°£¬ŌņÓŠŅ»øöøŚĪ»2ČĖ²Ī¼Ó£¬
¹ŹÓŠ·ÖÅä·½°ø ![]() £ØÖÖ£©£»
£ØÖÖ£©£»
£Øii£©øł¾ŻĢāŅā£¬4øöøŚĪ»3øöČĖ²Ī¼Ó£¬ĒŅĆæČĖÉķ¼ę2Ö°£¬²»Ķ¬µÄ·ÖÅä·½°øÓŠ
![]() ©£Ø
©£Ø ![]() +
+ ![]() £Ø
£Ø ![]() ©
© ![]() £©£©=114£ØÖÖ£©
£©£©=114£ØÖÖ£©
”¾½āĪö”æ£Ø¢ń£©£Øi£©ŌŚ£Ø2x©1£©10ÖŠ£¬Įīx=2æÉµĆ a0+a1+a2+”+a10µÄÖµ£»£Øii£©Įīx©1=y£¬µĆ³ö£Ø1+2y£©10=a0+a1y+a2y2+”+a10y10£¬ĄūÓƶžĻīÕ¹æŖŹ½µÄĶØĻī¹«Ź½Ēó³öa7µÄÖµ£»£Ø¢ņ£©£Øi£©ĻČ“Ó5ČĖÖŠŃ”³ö2ČĖ²Ī¼ÓŅ»øöøŚĪ»£¬ŌŁ·Ö4×éČ«ÅÅĮŠ£»£Øii£©øł¾ŻĢāŅā£¬Ēó³ö4øöøŚĪ»£¬3ČĖÖŠĆæČĖÉķ¼ęĮ½Ö°µÄ²»Ķ¬·ÖÅä·½°ø£®


 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĻĀĮŠĆüĢā“ķĪóµÄŹĒ £Ø £©
A. Čē¹ūĘ½Ćę![]() Ę½Ćę
Ę½Ćę![]() £¬ÄĒĆ“Ę½Ćę
£¬ÄĒĆ“Ę½Ćę![]() ÄŚŅ»¶Ø“ęŌŚÖ±ĻßĘ½ŠŠÓŚĘ½Ćę
ÄŚŅ»¶Ø“ęŌŚÖ±ĻßĘ½ŠŠÓŚĘ½Ćę![]()
B. Čē¹ūĘ½Ćę![]() ²»“¹Ö±Ę½Ćę
²»“¹Ö±Ę½Ćę![]() £¬ÄĒĆ“Ę½Ćę
£¬ÄĒĆ“Ę½Ćę![]() ÄŚŅ»¶Ø²»“ęŌŚÖ±Ļß“¹Ö±ÓŚĘ½Ćę
ÄŚŅ»¶Ø²»“ęŌŚÖ±Ļß“¹Ö±ÓŚĘ½Ćę![]()
C. Čē¹ūĘ½Ćę![]() Ę½Ćę
Ę½Ćę![]() £¬Ę½Ćę
£¬Ę½Ćę![]() Ę½Ćę
Ę½Ćę![]() £¬ĒŅ
£¬ĒŅ![]() £¬ÄĒĆ“
£¬ÄĒĆ“![]()
D. Čē¹ūĘ½Ćę![]() Ę½Ćę
Ę½Ćę![]() £¬ÄĒĆ“Ę½Ćę
£¬ÄĒĆ“Ę½Ćę![]() ÄŚĖłÓŠÖ±Ļ߶¼“¹Ö±ÓŚĘ½Ćę
ÄŚĖłÓŠÖ±Ļ߶¼“¹Ö±ÓŚĘ½Ćę![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖÖ±Ļßl¹żµćA(2,4)£¬ĒŅ±»Ę½ŠŠÖ±Ļßl1£ŗx£y£«1£½0Óėl2£ŗx£y£1£½0Ėł½ŲµÄĻ߶ĪÖŠµćMŌŚÖ±Ļßx£«y£3£½0ÉĻ£¬ĒóÖ±ĻßlµÄ·½³Ģ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĻĀĮŠĄż×ÓÖŠĖ껜±äĮæ¦Ī·ž“Ó¶žĻī·Ö²¼µÄÓŠ________£®
¢ŁĖ껜±äĮæ¦Ī±ķŹ¾ÖŲø“Å×ÖĄŅ»Ć¶÷»×Ón“ĪÖŠ³öĻֵ揿ŹĒ3µÄ±¶ŹżµÄ“ĪŹż£»
¢ŚÄ³ÉäŹÖ»÷ÖŠÄæ±źµÄøÅĀŹĪŖ0.9£¬“ÓæŖŹ¼Éä»÷µ½»÷ÖŠÄæ±źĖłŠčµÄÉä»÷“ĪŹż¦Ī£»
¢ŪÓŠŅ»Åś²śĘ·¹²ÓŠN¼ž£¬ĘäÖŠM¼žĪŖ“ĪĘ·£¬²ÉÓĆÓŠ·Å»Ų³éČ”·½·Ø£¬¦Ī±ķŹ¾n“Ī³éȔ֊³öĻÖ“ĪĘ·µÄ¼žŹż£ØM<N£©£»
¢ÜÓŠŅ»Åś²śĘ·¹²ÓŠN¼ž£¬ĘäÖŠM¼žĪŖ“ĪĘ·£¬²ÉÓĆ²»·Å»Ų³éČ”·½·Ø£¬¦Ī±ķŹ¾n“Ī³éȔ֊³öĻÖ“ĪĘ·µÄ¼žŹż£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¶ØŅåŌŚRÉĻµÄæɵ¼ŗÆŹżf£Øx£©Āś×ćf£Øx£©©f£Ø©x£©=2x3 £¬ µ±x”Ź£Ø©”Ž£¬0]Ź±f'£Øx£©£¼3x2 £¬ ŹµŹżaĀś×ćf£Ø1©a£©©f£Øa£©”Ż©2a3+3a2©3a+1£¬ŌņaµÄȔֵ·¶Ī§ŹĒ£Ø £©
A.![]()
B.![]()
C.![]()
D.![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖa£¼©1£¬ŗÆŹżf£Øx£©=|x3©1|+x3+ax£Øx”ŹR£©£®
£Ø¢ń£©ĒóŗÆŹżf£Øx£©µÄ×īŠ”Öµ£»
£Ø¢ņ£©ŅŃÖŖ“ęŌŚŹµŹżm£¬n£Øm£¼n”Ü1£©£¬¶ŌČĪŅāt0”Ź£Øm£¬n£©£¬×Ü“ęŌŚĮ½øö²»Ķ¬µÄt1 £¬ t2”Ź£Ø1£¬+”Ž£©£¬
Ź¹µĆf£Øt0£©©2=f£Øt1£©=f£Øt2£©£¬ĒóÖ¤£ŗ ![]() £®
£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖĶÖŌ²C£ŗ ![]() +
+ ![]() =1£Øa£¾b£¾0£©µÄ×ó”¢ÓŅ½¹µć·Ö±šĪŖF1”¢F2 £¬ ½¹¾ąĪŖ2£¬¹żµćF2×÷Ö±Ļßl½»ĶÖŌ²ÓŚM”¢NĮ½µć£¬”÷F1MNµÄÖܳ¤ĪŖ8£®
=1£Øa£¾b£¾0£©µÄ×ó”¢ÓŅ½¹µć·Ö±šĪŖF1”¢F2 £¬ ½¹¾ąĪŖ2£¬¹żµćF2×÷Ö±Ļßl½»ĶÖŌ²ÓŚM”¢NĮ½µć£¬”÷F1MNµÄÖܳ¤ĪŖ8£® 
£Ø¢ń£©ĒóĶÖŌ²CµÄ·½³Ģ£»
£Ø¢ņ£©ČōÖ±Ļßl·Ö±š½»Ö±Ļßy= ![]() x£¬y=©
x£¬y=© ![]() xÓŚP£¬QĮ½µć£¬Ēó
xÓŚP£¬QĮ½µć£¬Ēó ![]() µÄȔֵ·¶Ī§£®
µÄȔֵ·¶Ī§£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĻÖÓŠÄ³Åś“ĪĶ¬Ņ»ŠĶŗŵIJśĘ·¹²10¼ž£¬ĘäÖŠÓŠ8¼žŗĻøńĘ·£¬2¼ž“ĪĘ·£®
£Ø¢ń£©Ä³¼ģŃéŌ±“ÓÖŠÓŠ·Å»ŲµŲĮ¬Šų³éČ”²śĘ·2“Ī£¬Ćæ“ĪĖ껜³éČ”1¼ž£¬ĒóĮ½“Ī¶¼Č”µ½“ĪĘ·µÄøÅĀŹ£»
£Ø¢ņ£©ČōøĆ¼ģŃéŌ±“ÓÖŠČĪŅā³éČ”2¼ž£¬ÓĆX±ķŹ¾Č”³öµÄ2¼ž²śĘ·ÖŠ“ĪĘ·µÄ¼žŹż£¬ĒóXµÄ·Ö²¼ĮŠ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ¼«µćÓėÖ±½Ē×ų±źĻµµÄŌµćÖŲŗĻ£¬¼«ÖįÓėxÖįµÄÕż°ėÖįÖŲŗĻ£¬Ō²CµÄ¼«×ų±źŹĒ¦Ń=2asin¦Č£¬Ö±ĻßlµÄ²ĪŹż·½³ĢŹĒ 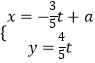 £ØtĪŖ²ĪŹż£©£®
£ØtĪŖ²ĪŹż£©£®
£Ø1£©Čōa=2£¬MĪŖÖ±ĻßlÓėxÖįµÄ½»µć£¬NŹĒŌ²CÉĻŅ»¶Æµć£¬Ēó|MN|µÄ×ī“óÖµ£»
£Ø2£©ČōÖ±Ļßl±»Ō²C½ŲµĆµÄĻŅ³¤ĪŖ ![]() £¬ĒóaµÄÖµ£®
£¬ĒóaµÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com