分析:(1)先求出导函数进而求出切线的斜率,再把1,2代入就可求出求x1、x2的值.求出点Pn的切线ln的方程即可求出及数列{xn}的通项公式;
(2)直接利用定积分来求Sn的表达式即可;
(3)利用(2)的结论先求出数列{Sn}的前n项之和为Tn,再把所要证明的结论转化为用数学归纳法证明en+1>(e-1)n+e即可
解答:解:(1)y′=-e
-x,设l
n的斜率为k
n,则
kn=-e-xn∴l
0的方程为:y=-x+1,令y=0得x
1=1,∴y
1=-e
-1P
1(1,e
-1),
k1=-e-x1=-e-1∴l
1的方程为:y-e
-1=-e
-1(x-1),令y=0得x
2=2,
一般地,l
n的方程为:
y-e-xn=-e-xn(x-xn),由Q
n+1(x
n+1,0)∈l
n得:x
n+1-x
n=1,∴x
n=n (4分)
(2)
Sn=e-xdx-(xn+1-xn)yn=-e-x-yn=(-e-n-1+e-n)-e-n=
•(8分)
(3)
Tn=•(+++)=•=•(1-)===1+,
==1+∴要证:
<,只要证明:
<,
即只要证明e
n+1>(e-1)n+e(10分)
证明;数学归纳法:
(一)当n=1时,显然(e-1)
2>0?e
2>2e-1?e
2>(e-1)+e成立
(二)假设n=k时,有e
k+1>(e-1)k+e
当n=k+1时,e
k+2=e•e
k+1>e[(e-1)k+e]
而e[(e-1)k+e]-[(e-1)(k+1)+e]=(e-1)
2(k+1)>0
∴e
k+2=e•e
k+1>e[(e-1)k+e]>(e-1)(k+1)+e
这说明n=k+1时不等式也成立,由(一)(二)知
<对一切正整数n都成立.
点评:一般在作数列与函数的综合题时,多用到数学归纳法的应用,所以要把这几个知识点掌握好.

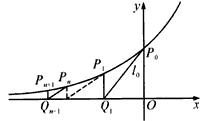
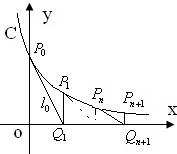 如图,过曲线C:y=e-x上一点P0(0,1)做曲线C的切线l0交x轴于Q1(x1,0)点,又过Q1做x轴的垂线交曲线C于P1(x1,y1)点,然后再过P1(x1,y1)做曲线C的切线l1交x轴于Q2(x2,0),又过Q2做x轴的垂线交曲线C于P2(x2,y2),…,以此类推,过点Pn的切线ln与x轴相交于点Qn+1(xn+1,0),再过点Qn+1做x轴的垂线交曲线C于点Pn+1(xn+1,yn+1)(n=1,2,3,…).
如图,过曲线C:y=e-x上一点P0(0,1)做曲线C的切线l0交x轴于Q1(x1,0)点,又过Q1做x轴的垂线交曲线C于P1(x1,y1)点,然后再过P1(x1,y1)做曲线C的切线l1交x轴于Q2(x2,0),又过Q2做x轴的垂线交曲线C于P2(x2,y2),…,以此类推,过点Pn的切线ln与x轴相交于点Qn+1(xn+1,0),再过点Qn+1做x轴的垂线交曲线C于点Pn+1(xn+1,yn+1)(n=1,2,3,…).

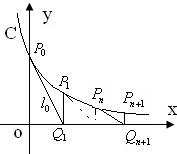 如图,过曲线C:y=e-x上一点P0(0,1)做曲线C的切线l0交x轴于Q1(x1,0)点,又过Q1做x轴的垂线交曲线C于P1(x1,y1)点,然后再过P1(x1,y1)做曲线C的切线l1交x轴于Q2(x2,0),又过Q2做x轴的垂线交曲线C于P2(x2,y2),…,以此类推,过点Pn的切线ln与x轴相交于点Qn+1(xn+1,0),再过点Qn+1做x轴的垂线交曲线C于点Pn+1(xn+1,yn+1)(n=1,2,3,…).
如图,过曲线C:y=e-x上一点P0(0,1)做曲线C的切线l0交x轴于Q1(x1,0)点,又过Q1做x轴的垂线交曲线C于P1(x1,y1)点,然后再过P1(x1,y1)做曲线C的切线l1交x轴于Q2(x2,0),又过Q2做x轴的垂线交曲线C于P2(x2,y2),…,以此类推,过点Pn的切线ln与x轴相交于点Qn+1(xn+1,0),再过点Qn+1做x轴的垂线交曲线C于点Pn+1(xn+1,yn+1)(n=1,2,3,…).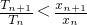 (n∈N+).
(n∈N+).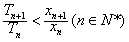 。
。 
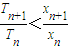 (n∈N+).
(n∈N+).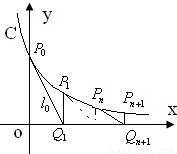
 (n∈N+).
(n∈N+).