

 •
• x•(1-x)•x=
x•(1-x)•x= (-x3+x2)(0<x<1)…4分
(-x3+x2)(0<x<1)…4分 x(x-
x(x- )
) 时,V′>0,
时,V′>0, <x<1时,V′<0…2分
<x<1时,V′<0…2分 时,V取得极大值,极大值为
时,V取得极大值,极大值为
 时,V有最大值为
时,V有最大值为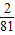 …2分
…2分

 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省高考模拟预测卷理科数学试卷(二)(解析版) 题型:解答题
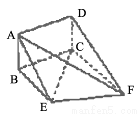
如图,矩形ABCD和梯形BEFC所在平面互相垂直,BE//CF,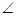 BCF=
BCF=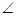 CEF=
CEF=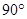 ,AD=
,AD=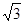 ,EF=2.
,EF=2.
(Ⅰ)求证:AE//平面DCF;
(Ⅱ)当AB的长为何值时,二面角A-EF-C的大小为 .
.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年宁夏高三第五次月考数学理卷 题型:解答题
(本小题满分12分)
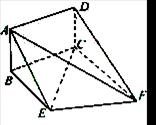
如图,矩形ABCD和梯形BEFC所在平面互相垂直,BE//CF,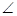 BCF=
BCF=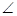 CEF=
CEF= ,AD=
,AD=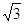 ,EF=2.
,EF=2.
(1)求证:AE//平面DCF;
(2)当AB的长为何值时,二面角A-EF-C的大小为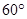 .
.
查看答案和解析>>
科目:高中数学 来源:2010-2011年河北省高二下学期期中考试理科数学 题型:解答题
(本小题满分12分)
如图,矩形ABCD和梯形BEFC所在平面互相垂直,BE//CF,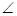 BCF=
BCF=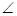 CEF=
CEF=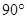 ,AD=
,AD=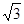 ,EF=2.
,EF=2.

(1)求证:AE//平面DCF;
(2)当AB的长为何值时,二面角A-EF-C的大小为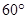 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
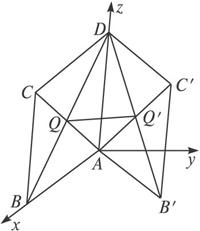
(1)求证:QQ′∥平面ABB′;
(2)当b=![]() a,且α=
a,且α=![]() 时,求异面直线AC与DB′所成的角;
时,求异面直线AC与DB′所成的角;
(3)当a>b,且AC⊥DB′时,求二面角α的余弦值(用a,b表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com