
����Ŀ���䳲���ɹ�����ڷ������ɵ�.�����濴���䳲�����������������ε��п���״�����Ӷ��ɣ��п���״��ĵײ���������ȫ�ȵ������湹��.��ͼ������������![]() ����������
����������![]() ���ֱ���ƽ��
���ֱ���ƽ��![]() ��ƽ��
��ƽ��![]() ��ƽ��
��ƽ��![]() �ص�������ȵ�����
�ص�������ȵ�����![]() ��
��![]() ��
��![]() ��ƽ��
��ƽ��![]() ��ƽ��
��ƽ��![]() ��ƽ��
��ƽ��![]() ���ڵ�
���ڵ�![]() �����γ��˷䳲�Ľṹ������ͼ��4����ʾ��
�����γ��˷䳲�Ľṹ������ͼ��4����ʾ��
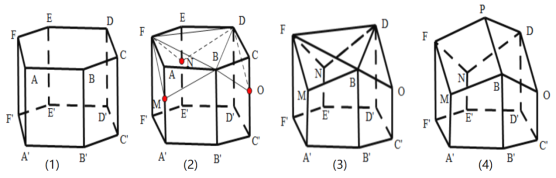
��ʿ��ѧ�ҿ�����������ֵķ���֤���˷䳲�����ֽṹ������ͬ�ݻ������ò�����ʡ�ģ�Ӣ����ѧ���������ͨ������õ����ε�һ���ڽ�Ϊ![]() ����
����![]() .�����������ۢ�
.�����������ۢ�![]() ����
���� ![]()
![]()
![]() ����
����![]() �ĵ㹲�棬��ȷ����ĸ���Ϊ______������
�ĵ㹲�棬��ȷ����ĸ���Ϊ______������![]() ��
��![]() ��
��![]() ����˷䳲�ı����Ϊ_______.
����˷䳲�ı����Ϊ_______.
���𰸡�2 ![]()
��������
�����������������������ε����ʿ��жϳ���֮��Ĵ�С��ϵ��ƽ�й�ϵ��������֪�������������ߵij��ȣ��䳲�ı��������6�����κ�3��������ɣ��ֱ�������κ����ε�������뼴��.
����ɵã�![]() ��
��
������![]() ����������
����������
����![]() ������
������![]() ��
��
���Ԣٴ���
��ƽ��![]() ��ƽ��
��ƽ��![]() ��ƽ��
��ƽ��![]() �ص�
�ص�
������ȵ�����![]() ��
��![]() ��
��![]() ��
��
����ƽ��![]() �����ƽ�У�
�����ƽ�У�
������![]() ��
��![]() ��
��![]() ,
,
����������![]() ��
��![]() ��
��
����![]()
![]()
![]() ������ȷ��
������ȷ��
��Ϊ![]() ��
��
����![]() ����
����![]() �ĵ㹲�棬����ȷ��
�ĵ㹲�棬����ȷ��
�����ȷ������2����
����![]() ��
��![]() ����ͼ��
����ͼ��

������ɵã�![]() ��
��![]() ��
��
��Ϊ![]() ��
��![]() ��
��
����![]() ��
��
����![]() ��
��
�ı���![]() Ϊ���Σ�
����
������![]() ����
����![]() ��
��
![]() ��
��
����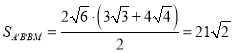 ��
��
![]() ��
��
���Է䳲�ı����Ϊ![]()
�ʴ�Ϊ��![]()


 ���ʿ��ÿ��ֳɳ�ϵ�д�
���ʿ��ÿ��ֳɳ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͳ�ƾֽ��е��Ĵξ����ղ飬ij���������15�����������10��Ƿ���������5��ƶ��������ѡȡ6����Ϊ�����ۺ��Ե������Ȼ������ȷ���ղ�����ֱ��������ղ�С��.�ղ����������Ҫ����������ѵ��Ȼ��ȷ����������뻧�Ǽǣ���������������ܻᵼ���뻧�ǼDz���˳������Ϊ��ʽ�ղ��ṩ�˱�����Ե㾭�飬��ij�ղ�С��������50������ҵ��λ��150�Ҹ��徭Ӫ�����ղ�������±���ʾ��
�ղ������� | ˳�� | ��˳�� | �ϼ� |
����ҵ��λ | 40 | 10 | 50 |
���徭Ӫ�� | 90 | 60 | 150 |
�ϼ� | 130 | 70 | 200 |
��1��д��ѡ��6�������ۺ��Ե�������õij���������
��2�������������ж��Ƿ���97.5%�İ�����Ϊ�����ղ�С�����뻧�Ǽ��Ƿ�˳�����ղ���������йء������������������ԭ��������������.
�����ο���ʽ��![]() ������
������![]()
�ο����ݣ�
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() Ϊʵ��������
Ϊʵ��������![]() ��
��
����������![]() �ĵ������䣻
�ĵ������䣻
����������![]() ��
��![]() �ϵ���Сֵ
�ϵ���Сֵ![]() ��
��
��������![]() ����ʹ����
����ʹ����![]() ��Ψһ���
��Ψһ���![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����к�����Ϊ�溯�����ǣ� ��
A.y��x2��2xB.y��x2cosxC.y��2x+2��xD.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ABC��A1B1C1�������ⳤ����ȣ�ƽ��BB1C1C��ƽ��ABC��BC1��C1C��
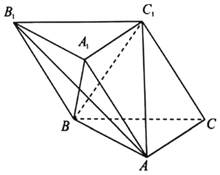
��1����֤��A1B��ƽ��AB1C1��
��2��������A1��AC1��B1������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У�����Խ���BD��![]() ������
������![]() ��ʹ�õ�
��ʹ�õ�![]() ��ƽ��ABCD�ڵ���ӰǡΪ��B����EΪ
��ƽ��ABCD�ڵ���ӰǡΪ��B����EΪ![]() ���е㣮
���е㣮
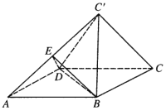
������֤��![]() ƽ��BDE��
ƽ��BDE��
������![]() ����
����![]() ��ƽ��BDE���ɵĽǣ�
��ƽ��BDE���ɵĽǣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����н�������ȷ�ĸ���Ϊ�� ��
(1)![]() ��ֱ��
��ֱ��![]() ��ֱ��
��ֱ��![]() ��ֱ�ij�Ҫ������
��ֱ�ij�Ҫ������
(2)�����Իع鷽����,���ϵ��![]() Խ��,������������Խǿ��
Խ��,������������Խǿ��
(3)��֪�������![]() ,��
,��![]() ,��
,��![]()
(4)������![]() ,
,![]() ,��
,��![]() ,
,![]()
A.1B.2C.3D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ����
����![]() ��
��![]() �ֱ�Ϊ��ԲC�����ҽ�����
�ֱ�Ϊ��ԲC�����ҽ�����![]() .
.
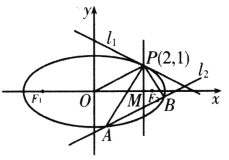
��1������ԲC�ķ��̣�
��2����P���ֱ��![]() ����ԲC����ֻ��һ�������㣬ֱ��
����ԲC����ֻ��һ�������㣬ֱ��![]() ƽ����OP��OΪԭ�㣩��������ԲC��������A��B����ֱ��
ƽ����OP��OΪԭ�㣩��������ԲC��������A��B����ֱ��![]() ���ڵ�M��M����A��B����֮�䣩.
���ڵ�M��M����A��B����֮�䣩.
��i����![]() ������ʱ����
������ʱ����![]() �ķ��̣�
�ķ��̣�
��ii����֤��![]() �����ж�
�����ж�![]() ��
��![]() ��б���Ƿ����ij��˳�ɵȱ�����.
��б���Ƿ����ij��˳�ɵȱ�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ȫ�濹���¹ڷ���������һ����ʱ�ڣ����н����������ͣ�β�ͣѧ���Ŀںţ�����ѧ������ѧϰ.ijУ��ѧ��ʦΪ�˵������ѧ����ѧ�ɼ�������ѧϰʱ��֮�����ع�ϵ���Ը����꼶���ѡȡ45��ѧ�����и����ʾ�������ÿ������ѧϰ��ѧʱ�䲻����5Сʱ����19�ˣ����µ����У��ڼ�⿼������ѧƽ���ɼ�����120�ֵ�ռ![]() ��ͳ�Ƴɼ���õ�����
��ͳ�Ƴɼ���õ�����![]() ��������
��������
����������120�� | ��������120�� | �ϼ� | |
����ѧϰʱ�䲻����5Сʱ | 4 | 19 | |
����ѧϰʱ�䲻��5Сʱ | |||
�ϼ� | 45 |
��1�����������![]() �����������ж��Ƿ���99%�İ�����Ϊ������ѧ������ѧ�ɼ���ѧ������ѧϰʱ���й�����
�����������ж��Ƿ���99%�İ�����Ϊ������ѧ������ѧ�ɼ���ѧ������ѧϰʱ���й�����
��2�������������дӷ���������120�ֵ�ѧ���У����շֲ�����ķ������鵽����ѧϰʱ�䲻����5Сʱ������ѧϰʱ�䲻��5Сʱ��ѧ����5����������5��ѧ���������ȡ2�ˣ�������1��ÿ������ѧϰʱ�䲻��5Сʱ�ĸ���.
��������ٽ�ֵ�����ο���
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
���ο���ʽ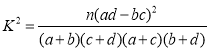 ����
����![]() ��
��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com