
【题目】选修4-5:不等式选讲
已知不等式![]()
![]() 对任意实数
对任意实数![]() 恒成立.
恒成立.
(Ⅰ)求实数![]() 的最小值
的最小值![]() ;
;
(Ⅱ)若![]() ,且满足
,且满足![]() ,求证:
,求证:![]() .
.
科目:高中数学 来源: 题型:
【题目】某厂生产某种产品x(百台),总成本为C(x)(万元),其中固定成本为2万元,每生产1百台,成本增加1万元,销售收入 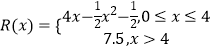 (万元),假定该产品产销平衡.
(万元),假定该产品产销平衡.
(1)若要该厂不亏本,产量x应控制在什么范围内?
(2)该厂年产多少台时,可使利润最大?
(3)求该厂利润最大时产品的售价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产一种产品,第一年投入资金1000万元,出售产品收入40万元,预计以后每年的投入资金是上一年的一半,出售产品所得收入比上一年多80万元,同时,当预计投入的资金低于20万元时,就按20万元投入,且当年出售产品收入与上一年相等.
(1)求第![]() 年的预计投入资金与出售产品的收入;
年的预计投入资金与出售产品的收入;
(2)预计从哪一年起该公司开始盈利?(注:盈利是指总收入大于总投入)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,函数
,函数![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若关于![]() 的方程
的方程![]() 的解集中恰有一个元素,求
的解集中恰有一个元素,求![]() 的取值范围;
的取值范围;
(3)设![]() ,若对任意
,若对任意![]() ,函数
,函数![]() 在区间
在区间![]() 上的最大值与最小值的差不超过1,求
上的最大值与最小值的差不超过1,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() .
.
(Ⅰ)求函数f(x)的定义域;
(Ⅱ)判定f(x)的奇偶性并证明;
(Ⅲ)用函数单调性定义证明:f(x)在(1,+∞)上是增函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某城市气象部门的数据中,随机抽取了100天的空气质量指数的监测数据如表:
空气质量指数t | (0,50] | (50,100] | (100,150] | (150,200] | (200,300] | |
质量等级 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 严重污染 |
天数K | 5 | 23 | 22 | 25 | 15 | 10 |
(1)在该城市各医院每天收治上呼吸道病症总人数y与当天的空气质量t(t取整数)存在如下关系y=![]() ,且当t>300时,y>500估计在某一医院收治此类病症人数超过200人的概率;
,且当t>300时,y>500估计在某一医院收治此类病症人数超过200人的概率;
(2)若在(1)中,当t>300时,y与t的关系拟合于曲线![]() ,现已取出了10对样本数据(ti,yi)(i=1,2,3,…,10),且
,现已取出了10对样本数据(ti,yi)(i=1,2,3,…,10),且![]() ,求拟合曲线方程.
,求拟合曲线方程.
(附:线性回归方程![]() =a+bx中,b=
=a+bx中,b= ,a=
,a=![]() ﹣b
﹣b![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,分别根据下列条件解三角形,其中有两个解的是( )
A.a=7,b=14,A=30°
B.a=20,b=26,A=150°
C.a=30,b=40,A=30°
D.a=72,b=60,A=135°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一(2)班共有60名同学参加期末考试,现将其数学学科成绩(均为整数)分成六个分数段![]() ,
, ![]() ,…,
,…, ![]() ,画出如下图所示的部分频率分布直方图,请观察图形信息,回答下列问题:
,画出如下图所示的部分频率分布直方图,请观察图形信息,回答下列问题:
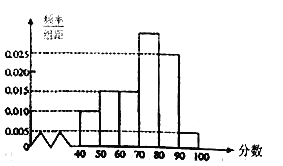
(1)估计这次考试中数学学科成绩的中位数;
(2)现根据本次考试分数分成下列六段(从低分段到高分段依次为第一组、第二组、…、第六组)为提高本班数学整体成绩,决定组与组之间进行帮扶学习.若选出的两组分数之差大于30分(以分数段为依据,不以具体学生分数为依据),则称这两组为“最佳组合”,试求选出的两组为“最佳组合”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在明朝程大位《算法统宗》中,有这样的一首歌谣,叫做浮屠增级歌.“远看巍巍塔七层,红光点点倍加倍;共灯三百八十一,请问尖头几盏灯?”本题是说,“远处有一座雄伟的佛塔,塔上挂满了许多红灯,下一层灯数是上一层灯数的2倍,全塔共有381盏,试问顶层有几盏灯?”;同样在这本书中还有一道著名算题:“一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁?”如果译成白话文,其意思是:“有100个和尚分100个馒头,如果大和尚一人分3个,小和尚3人分一个,正好分完.”现按照分层抽样的办法从这100名和尚中选取12人派去布置第一个问题中最顶层的灯,那么每盏灯需要分派的大小和尚数各为(A)1人,3人 (B)2人,4人 (C)3人,6人 (D)3人,9人
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com