
【题目】已知![]() ,(其中常数
,(其中常数![]() ).
).
(1)当![]() 时,求函数
时,求函数![]() 的极值;
的极值;
(2)若函数![]() 有两个零点
有两个零点![]() ,求证:
,求证:![]() .
.
【答案】(1)![]() 有极小值
有极小值![]() ,无极大值;(2)证明见解析.
,无极大值;(2)证明见解析.
【解析】
(1)求出a=e的函数的导数,求出单调区间,即可求得极值;(2)先证明:当f(x)≥0恒成立时,有 0<a≤e成立.若![]() ,则f(x)=ex﹣a(lnx+1)≥0显然成立;若
,则f(x)=ex﹣a(lnx+1)≥0显然成立;若![]() ,运用参数分离,构造函数通过求导数,运用单调性,结合函数零点存在定理,即可得证.
,运用参数分离,构造函数通过求导数,运用单调性,结合函数零点存在定理,即可得证.
函数![]() 的定义域为
的定义域为![]() ,
,
(1)当![]() 时,
时,![]() ,
,![]() ,
,![]() 在
在![]() 单调递增且
单调递增且![]()
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() 有极小值
有极小值![]() ,无极大值.
,无极大值.
(2)先证明:当![]() 恒成立时,有
恒成立时,有![]() 成立
成立
若![]() ,则
,则![]() 显然成立;
显然成立;
若![]() ,由
,由![]() 得
得![]() ,令
,令![]() ,则
,则![]() ,
,
令![]() ,由
,由![]() 得
得![]() 在
在![]() 上单调递增,
上单调递增,
又∵![]() ,所以
,所以![]() 在
在![]() 上为负,递减,在
上为负,递减,在![]() 上为正,递增,∴
上为正,递增,∴ ![]() ,从而
,从而![]() .
.
因而函数![]() 若有两个零点,则
若有两个零点,则![]() ,所以
,所以![]() ,
,
由![]() 得
得![]() ,则
,则![]() ,
,
∴![]() 在
在![]() 上单调递增,∴
上单调递增,∴![]() ,
,
∴![]() 在
在![]() 上单调递增∴
上单调递增∴![]() ,则
,则![]()
∴![]() ,由
,由![]() 得
得![]() ,
,
则![]() ,∴
,∴![]() ,综上
,综上![]() .
.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:
【题目】一批用于手电筒的电池,每节电池的寿命服从正态分布![]() (寿命单位:小时).考虑到生产成本,电池使用寿命在
(寿命单位:小时).考虑到生产成本,电池使用寿命在![]() 内是合格产品.
内是合格产品.
(1)求一节电池是合格产品的概率(结果四舍五入,保留一位小数);
(2)根据(1)中的数据结果,若质检部门检查4节电池,记抽查电池合格的数量为![]() ,求随机变量
,求随机变量![]() 的分布列、数学期望及方差.
的分布列、数学期望及方差.
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,过点
中,过点![]() 作倾斜角为
作倾斜角为![]() 的直线
的直线![]() ,以原点
,以原点![]() 为极点,
为极点,![]() 轴非负半轴为极轴建立极坐标系,曲线
轴非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,将曲线
,将曲线![]() 上各点的横坐标伸长为原来的2倍,纵坐标不变,得到曲线
上各点的横坐标伸长为原来的2倍,纵坐标不变,得到曲线![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于不同的两点
交于不同的两点![]() .
.
(1)求直线![]() 的参数方程和曲线
的参数方程和曲线![]() 的普通方程;
的普通方程;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国在欧洲的某孔子学院为了让更多的人了解中国传统文化,在当地举办了一场由当地人参加的中国传统文化知识大赛,为了了解参加本次大赛参赛人员的成绩情况,从参赛的人员中随机抽取![]() 名人员的成绩(满分100分)作为样本,将所得数据进行分析整理后画出频率分布直方图如图所示,已知抽取的人员中成绩在[50,60)内的频数为3.
名人员的成绩(满分100分)作为样本,将所得数据进行分析整理后画出频率分布直方图如图所示,已知抽取的人员中成绩在[50,60)内的频数为3.
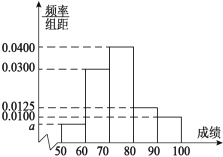
(1)求![]() 的值和估计参赛人员的平均成绩(保留小数点后两位有效数字);
的值和估计参赛人员的平均成绩(保留小数点后两位有效数字);
(2)已知抽取的![]() 名参赛人员中,成绩在[80,90)和[90,100]女士人数都为2人,现从成绩在[80,90)和[90,100]的抽取的人员中各随机抽取2人,记这4人中女士的人数为
名参赛人员中,成绩在[80,90)和[90,100]女士人数都为2人,现从成绩在[80,90)和[90,100]的抽取的人员中各随机抽取2人,记这4人中女士的人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三1班共有48人,在“六选三”时,该班共有三个课程组合:理化生、理化历、史地政其中,选择理化生的共有24人,选择理化历的共有16人,其余人选择了史地政,现采用分层抽样的方法从中抽出6人,调查他们每天完成作业的时间.
(1)应从这三个组合中分别抽取多少人?
(2)若抽出的6人中有4人每天完成六科(含语数英)作业所需时间在3小时以上,2人在3小时以内.现从这6人中随机抽取3人进行座谈.
用X表示抽取的3人中每天完成作业所需时间在3小时以上的人数,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() .
.
(1)若![]() ,求函数
,求函数![]() 的单调区间;
的单调区间;
(2)若![]() ,且函数
,且函数![]() 在区间
在区间![]() 内有两个极值点,求实数a的取值范围;
内有两个极值点,求实数a的取值范围;
(3)求证:对任意的正数a,都存在实数t,满足:对任意的![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com