
【题目】已知函数![]() ,
, ![]() .
.
(1)求函数![]() 在点
在点![]() 点处的切线方程;
点处的切线方程;
(2)当![]() 时,求函数
时,求函数![]() 的极值点和极值;
的极值点和极值;
(3)当![]() 时,
时, ![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() 的极大值
的极大值![]() ,函数无极小值;(3)
,函数无极小值;(3)![]() .
.
【解析】试题分析:1)求出导函数,求解切线的斜率f′(1)=1﹣a,然后求解切线方程;
(2)求出函数的极值点,判断函数的单调性,求解函数的极值即可;
(3)令g(x)=xlnx﹣a(x2﹣1)(x≥1),求出导函数g′(x)=lnx+1﹣2ax,令F(x)=g′(x)=lnx+1﹣2ax,求出![]() ,通过若a≤0,若
,通过若a≤0,若![]() ,若
,若![]() ,分别判断函数的符号函数的单调性,求解函数的最值,然后求解a的取值范围.
,分别判断函数的符号函数的单调性,求解函数的最值,然后求解a的取值范围.
试题解析:
(1)由题![]() ,所以
,所以![]() ,
,
所以切线方程为: ![]()
(2)由题![]() 时,
时, ![]() ,所以
,所以![]()
所以![]() ;
; ![]() ,
,
所以![]() 在
在![]() 单增,在
单增,在![]() 单减,所以
单减,所以![]() 在
在![]() 取得极大值
取得极大值![]() .
.
所以函数![]() 的极大值
的极大值![]() ,函数无极小值
,函数无极小值
(3)![]() ,令
,令![]() ,
,
![]() ,令
,令![]() ,
, ![]()
(1)若![]() ,
, ![]() ,
, ![]() 在
在![]() 递增,
递增, ![]()
∴![]() 在
在![]() 递增,
递增, ![]() ,从而
,从而![]() ,不符合题意
,不符合题意
(2)若![]() ,当
,当![]() ,
, ![]() ,∴
,∴![]() 在
在![]() 递增,
递增,
从而![]() ,以下论证同(1)一样,所以不符合题意
,以下论证同(1)一样,所以不符合题意
(3)若![]() ,
, ![]() 在
在![]() 恒成立,
恒成立,
∴![]() 在
在![]() 递减,
递减, ![]() ,
,
从而![]() 在
在![]() 递减,∴
递减,∴![]() ,
, ![]() ,
,
综上所述, ![]() 的取值范围是
的取值范围是![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°. 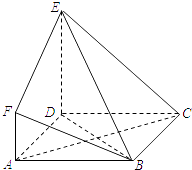
(1)求证:AC⊥平面BDE;
(2)设点M是线段BD上一个动点,试确定点M的位置,使得AM∥平面BEF,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年4月23日“世界读书日”来临之际,某校为了了解中学生课外阅读情况,随机抽取了100名学生,并获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表.
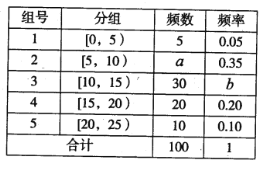
(Ⅰ)求![]() 的值,并作出这些数据的频率分布直方图;
的值,并作出这些数据的频率分布直方图;

(Ⅱ)假设每组数据组间是平均分布的,试估计该组数据的平均数;(同一组中的数据用该组区间的中点值作代表);
(Ⅲ)现从第3、4、5组中用分层抽样的方法抽取6人参加校“中华诗词比赛”,经过比赛后从这6人中选拔2人组成该校代表队,求这2人来自不同组别的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年4月23日“世界读书日”来临之际,某校为了了解中学生课外阅读情况,随机抽取了100名学生,并获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表.

(1)求![]() 的值,并作出这些数据的频率分布直方图;
的值,并作出这些数据的频率分布直方图;

(2)现从第3、4、5组中用分层抽样的方法抽取6人参加校“中华诗词比赛”,经过比赛后从这6人中选拔2人组成该校代表队,求这2人来自不同组别的概率;
(3)假设每组数据组间是平均分布的,若该校希望使15%的学生的一周课外阅读时间不低于![]() (小时)的时间,作为评选该校“课外阅读能手”的依据,试估计该值
(小时)的时间,作为评选该校“课外阅读能手”的依据,试估计该值![]() ,并说明理由.
,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司计划投资A、B两种金融产品,根据市场调查与预测,A产品的利润与投资量成正比例,其关系如图1,B产品的利润与投资量的算术平方根成正比例,其关系如图2(注:利润与投资量的单位:万元).
(1)分别将A、B两产品的利润表示为投资量的函数关系式;
(2)该公司已有10万元资金,并全部投入A、B两种产品中,问:怎样分配这10万元投资,才能使公司获得最大利润?其最大利润为多少万元?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,AB⊥平面BCP,CD∥平面ABP,AB=BC=CP=BP=2CD=2 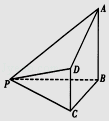
(1)证明:平面ABP⊥平面ADP;
(2)若直线PA与平面PCD所成角为α,求sinα的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近几年,京津冀等地数城市指数“爆表”,尤其2015年污染最重.为了探究车流量与![]() 的浓度是否相关,现采集到北方某城市2015年12月份某星期星期一到星期日某一时间段车流量与
的浓度是否相关,现采集到北方某城市2015年12月份某星期星期一到星期日某一时间段车流量与![]() 的数据如表:
的数据如表:
时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期七 |
车流量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 28 | 30 | 35 | 41 | 49 | 56 | 62 |
(1)由散点图知![]() 与
与![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于的线性回归方程;
(2)(ⅰ)利用(1)所求的回归方程,预测该市车流量为8万辆时![]() 的浓度;
的浓度;
(ⅱ)规定:当一天内![]() 的浓度平均值在
的浓度平均值在![]() 内,空气质量等级为优;当一天内
内,空气质量等级为优;当一天内![]() 的浓度平均值在
的浓度平均值在![]() 内,空气质量等级为良.为使该市某日空气质量为优或者为良,则应控制当天车流量在多少万辆以内?(结果以万辆为单位,保留整数.)
内,空气质量等级为良.为使该市某日空气质量为优或者为良,则应控制当天车流量在多少万辆以内?(结果以万辆为单位,保留整数.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com