
 ,m(x)=2lnx..
,m(x)=2lnx.. ,若对任意x1,x2∈[1,e],f(x1)-m(x1)<g(x2)成立,求实数p的取值范围.
,若对任意x1,x2∈[1,e],f(x1)-m(x1)<g(x2)成立,求实数p的取值范围. ,
, 令h(x)=px2-2x+p,当p≥1时,h(x)=px2-2x+p,其图象为开口向上的抛物线,对称轴为
令h(x)=px2-2x+p,当p≥1时,h(x)=px2-2x+p,其图象为开口向上的抛物线,对称轴为 ,由此能够证明f(x)>m(x).
,由此能够证明f(x)>m(x). 在[1,e]上是减函数,知g(x)∈[2,2e].当P=0时,h(x)=-2x,G(x)在(0,+∞)内是单调递减函数;当P<0时,h(x)=px2-2x+p,G(x)max=G(1)=0<2;当0<p<1时,
在[1,e]上是减函数,知g(x)∈[2,2e].当P=0时,h(x)=-2x,G(x)在(0,+∞)内是单调递减函数;当P<0时,h(x)=px2-2x+p,G(x)max=G(1)=0<2;当0<p<1时, ;当p≥1时,
;当p≥1时, .所以G(x)在[1,e]上为单调递增函数,由此能求出p的取值范围.
.所以G(x)在[1,e]上为单调递增函数,由此能求出p的取值范围. ,
, ,
, ,
,
 在[1,e]上是减函数,
在[1,e]上是减函数, ,
, ,
, ,
,
 ,
, ,
, ,g(x)min=2,
,g(x)min=2, )-2lne<2,
)-2lne<2, ,
, .
.

 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:
| 1 |
| 6 |
| 1 |
| 2 |
| A、既有极大值,也有极小值 |
| B、既有极大值,也有最小值 |
| C、有极大值,没有极小值 |
| D、没有极大值,也没有极小值 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2-1 |
| 1-x2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 ,m(x)=2lnx..
,m(x)=2lnx..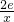 ,若对任意x1,x2∈[1,e],f(x1)-m(x1)<g(x2)成立,求实数p的取值范围.
,若对任意x1,x2∈[1,e],f(x1)-m(x1)<g(x2)成立,求实数p的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com