
【题目】已知函数![]() 是偶函数,且满足
是偶函数,且满足![]() ,当
,当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() 的最大值为
的最大值为![]() .
.
(1)求实数![]() 的值;
的值;
(2)函数![]() ,若对任意的
,若对任意的![]() ,总存在
,总存在![]() ,使不等式
,使不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)2;(2)![]() 或
或![]()
【解析】试题分析:
(1)由题意先求得函数具有性质![]() ,于是可得当
,于是可得当![]() 时,
时, ![]() ,利用导数可判断
,利用导数可判断![]() 在
在![]() 上单调递增,故
上单调递增,故![]() ,根据条件得到
,根据条件得到![]() .(2)由于“对任意的
.(2)由于“对任意的![]() ,总存在
,总存在![]() ,使不等式
,使不等式![]() 恒成立”等价于“
恒成立”等价于“![]() ”,故可将问题转化为求函数
”,故可将问题转化为求函数![]() 的最大值或其值域.
的最大值或其值域.
试题解析:
(1)∵![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() ,
,
当![]() 时,
时, ![]() ,
,
∴当![]() 时,
时, ![]() ,
,
∴![]() .
.
又![]() ,
,
∴![]() 恒成立,
恒成立,
∴![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() ,
,
令![]() ,解得
,解得![]() .
.
∴实数![]() 的值为2.
的值为2.
(2)当![]() 时,
时, ![]() ,
,
∴![]() ,
,
∴函数![]() 在
在![]() 单调递增,
单调递增,
∴当![]() 时,
时, ![]() .
.
又当![]() 时,
时, ![]() ,
,
∴![]() .
.
①当![]() 时,
时, ![]() ,函数
,函数![]() 在区间
在区间![]() 单调递增,
单调递增,
∴![]() .
.
∵对任意的![]() ,总存在
,总存在![]() ,使不等式
,使不等式![]() 恒成立,
恒成立,
∴![]()
解得![]() ;
;
②当![]() 时,
时, ![]() ,函数
,函数![]() 在区间
在区间![]() 单调递减,
单调递减,
∴![]() ,
,
同①可得![]() ,
,
解得![]() ;
;
综上![]() 或
或![]() .
.
∴实数![]() 的取值范围
的取值范围![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知某批零件的长度误差(单位:毫米)服从正态分布N(0,32),从中随机取一件,其长度误差落在区间(3,6)内的概率为( )
(附:若随机变量ξ服从正态分布N(μ,σ2),则P(μ-σ<ξ<μ+σ)=68.27%,P(μ-2σ<ξ<μ+2σ)=95.45%.)
A. 4.56%B. 13.59%C. 27.18%D. 31.74%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}是等差数列,a1=f(x+1),a2=0,a3=f(x-1),其中f(x)=x2-4x+2.
(1)求通项公式an;
(2)若数列{an}为递增数列,令bn=an+1+an+2+an+3+an+4,求数列{![]() }的前n项和Sn.
}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥A﹣BCD中,BCD是边长为![]() 的等边三角形,
的等边三角形,![]() ,二面角A﹣BC﹣D的大小为θ,且
,二面角A﹣BC﹣D的大小为θ,且![]() ,则三棱锥A﹣BCD体积的最大值为( )
,则三棱锥A﹣BCD体积的最大值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥![]() 的底面
的底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() 为正三角形.
为正三角形.
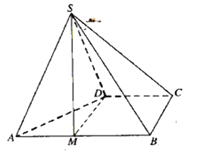
(1)点![]() 为棱
为棱![]() 上一点,若
上一点,若![]() 平面
平面![]() ,
,![]() ,求实数
,求实数![]() 的值;
的值;
(2)求点B到平面SAD的距离.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)由![]() 平面
平面![]() ,可证
,可证![]() ,进而证得四边形
,进而证得四边形![]() 为平行四边形,根据
为平行四边形,根据![]() ,可得
,可得![]() ;
;
(2)利用等体积法![]() 可求点
可求点![]() 到平面
到平面![]() 的距离.
的距离.
试题解析:((1)因为![]() 平面SDM,
平面SDM,
![]()
![]() 平面ABCD,
平面ABCD,
平面SDM ![]() 平面ABCD=DM,
平面ABCD=DM,
所以![]() ,
,
因为![]() ,所以四边形BCDM为平行四边形,又
,所以四边形BCDM为平行四边形,又![]() ,所以M为AB的中点.
,所以M为AB的中点.
因为![]() ,
,
![]() .
.

(2)因为![]()
![]() ,
, ![]()
![]() ,
,
所以![]() 平面
平面![]() ,
,
又因为![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,
在平面![]() 内过点
内过点![]() 作
作![]() 直线
直线![]() 于点
于点![]() ,则
,则![]() 平面
平面![]() ,
,
在![]() 和
和![]() 中,
中,
因为![]() ,所以
,所以![]() ,
,
又由题知![]() ,
,
所以![]() ,
,
由已知求得![]() ,所以
,所以![]() ,
,
连接BD,则![]() ,
,
又求得![]() 的面积为
的面积为![]() ,
,
所以由![]() 点B 到平面
点B 到平面![]() 的距离为
的距离为![]() .
.
【题型】解答题
【结束】
19
【题目】小明在石家庄市某物流派送公司找到了一份派送员的工作,该公司给出了两种日薪薪酬方案.甲方案:底薪100元,每派送一单奖励1元;乙方案:底薪140元,每日前55单没有奖励,超过55单的部分每单奖励12元.
(1)请分别求出甲、乙两种薪酬方案中日薪![]() (单位:元)与送货单数
(单位:元)与送货单数![]() 的函数关系式;
的函数关系式;
(2)根据该公司所有派送员100天的派送记录,发现派送员的日平均派送单数与天数满足以下表格:
日均派送单数 | 52 | 54 | 56 | 58 | 60 |
频数(天) | 20 | 30 | 20 | 20 | 10 |
回答下列问题:
①根据以上数据,设每名派送员的日薪为![]() (单位:元),试分别求出这100天中甲、乙两种方案的日薪
(单位:元),试分别求出这100天中甲、乙两种方案的日薪![]() 平均数及方差;
平均数及方差;
②结合①中的数据,根据统计学的思想,帮助小明分析,他选择哪种薪酬方案比较合适,并说明你的理由.
(参考数据: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M的圆心在直线![]() :
:![]() 上,与直线
上,与直线![]() :
:![]() 相切,截直线
相切,截直线![]() :
:![]() 所得的弦长为6.
所得的弦长为6.
(1)求圆M的方程;
(2)过点![]() 的两条成
的两条成![]() 角的直线分别交圆M于A,C和B,D,求四边形
角的直线分别交圆M于A,C和B,D,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,选项正确的是( )
A. 在回归直线![]() 中,变量
中,变量![]() 时,变量
时,变量![]() 的值一定是15
的值一定是15
B. 两个变量相关性越强,则相关系数![]() 就越接近于1
就越接近于1
C. 在残差图中,残差点比较均匀落在水平的带状区域中即可说明选用的模型比较合适,与带状区域的宽度无关
D. 若某商品的销售量![]() (件)与销售价格
(件)与销售价格![]() (元/件)存在线性回归方程为
(元/件)存在线性回归方程为![]() ,当销售价格为10元时,销售量为100件左右
,当销售价格为10元时,销售量为100件左右
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com