
【题目】已知a∈R,函数f(x)=ex﹣1﹣ax的图象与x轴相切. (Ⅰ)求f(x)的单调区间;
(Ⅱ)当x>1时,f(x)>m(x﹣1)lnx,求实数m的取值范围.
【答案】解:(Ⅰ)f′(x)=ex﹣1﹣a,设切点为(x0 , 0), 依题意, 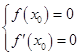 ,解得
,解得 ![]()
所以f′(x)=ex﹣1﹣1.
当x<1时,f′(x)<0;当x>1时,f′(x)>0.
故f(x)的单调递减区间为(﹣∞,1),单调递增区间为(1,+∞).
(Ⅱ)令g(x)=f(x)﹣m(x﹣1)lnx,x>0.
则g′(x)=ex﹣1﹣m(lnx+ ![]() )﹣1,
)﹣1,
令h(x)=g′(x),则h′(x)=ex﹣1﹣m( ![]() +
+ ![]() ),
),
(ⅰ)若m≤ ![]() ,
,
因为当x>1时,ex﹣1>1,m( ![]() +
+ ![]() )<1,所以h′(x)>0,
)<1,所以h′(x)>0,
所以h(x)即g′(x)在(1,+∞)上单调递增.
又因为g′(1)=0,所以当x>1时,g′(x)>0,
从而g(x)在[1,+∞)上单调递增,
而g(1)=0,所以g(x)>0,即f(x)>m(x﹣1)lnx成立.
(ⅱ)若m> ![]() ,
,
可得h′(x)在(0,+∞)上单调递增.
因为h′(1)=1﹣2m<0,h′(1+ln(2m))>0,
所以存在x1∈(1,1+ln(2m)),使得h′(x1)=0,
且当x∈(1,x1)时,h′(x)<0,所以h(x)即g′(x)在(1,x1)上单调递减,
又因为g′(1)=0,所以当x∈(1,x1)时,g′(x)<0,
从而g(x)在(1,x1)上单调递减,
而g(1)=0,所以当x∈(1,x1)时,g(x)<0,即f(x)>m(x﹣1)lnx不成立.
纵上所述,k的取值范围是(﹣∞, ![]() ]
]
【解析】(Ⅰ)求出函数的导数,根据函数图象与x轴相切,求出a的值,从而求出函数的单调区间;(Ⅱ)求出g(x)的导数,通过讨论m的范围,结合函数的单调性以及f(x)>m(x﹣1)lnx,求出m的范围即可.
【考点精析】本题主要考查了利用导数研究函数的单调性的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减才能正确解答此题.
在这个区间单调递减才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】学校举办的集体活动中,设计了如下有奖闯关游戏:参赛选手按第一关、第二关、第三关的顺序依次闯关,若闯关成功,分别获得1分、2分、3分的奖励,游戏还规定,当选手闯过一关后,可以选择得到相应的分数,结束游戏;也可以选择继续闯下一关,若有任何一关没有闯关成功,则全部分数都归零,游戏结束。设选手甲第一关、第二关、第三关的概率分别为![]() ,
,![]() ,
,![]() ,选手选择继续闯关的概率均为
,选手选择继续闯关的概率均为![]() ,且各关之间闯关成功互不影响
,且各关之间闯关成功互不影响
(I)求选手甲第一关闯关成功且所得分数为零的概率
(II)设该学生所得总分数为X,求X的分布列与数学期望
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.

(1)求证:PA⊥BD;
(2)求证:平面BDE⊥平面PAC;
(3)当PA∥平面BDE时,求三棱锥E-BCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明跟父母、爷爷奶奶一同参加《中国诗词大会》的现场录制,5人坐成一排.若小明的父母至少有一人与他相邻,则不同坐法的总数为
A. 60 B. 72 C. 84 D. 96
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】重庆一中为了增强学生的记忆力和辨识力,组织了一场类似《最强大脑》的![]() 赛,
赛,![]() 两队各由4名选手组成,每局两队各派一名选手
两队各由4名选手组成,每局两队各派一名选手![]() ,除第三局胜者得2分外,其余各局胜者均得1分,每局的负者得0分.假设每局比赛
,除第三局胜者得2分外,其余各局胜者均得1分,每局的负者得0分.假设每局比赛![]() 队选手获胜的概率均为
队选手获胜的概率均为![]() ,且各局比赛结果相互独立,比赛结束时
,且各局比赛结果相互独立,比赛结束时![]() 队的得分高于
队的得分高于![]() 队的得分的概率为( )
队的得分的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4﹣4:坐标系与参数方程 曲线C1的参数方程为 ![]() (α为参数),在以原点O为极点,x轴的正半轴为极轴的极坐标系中,曲线C2的极坐标方程为ρcos2θ=sinθ.
(α为参数),在以原点O为极点,x轴的正半轴为极轴的极坐标系中,曲线C2的极坐标方程为ρcos2θ=sinθ.
(1)求曲线C1的极坐标方程和曲线C2的直角坐标方程;
(2)若射线l:y=kx(x≥0)与曲线C1 , C2的交点分别为A,B(A,B异于原点),当斜率k∈(1, ![]() ]时,求|OA||OB|的取值范围.
]时,求|OA||OB|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】非空数集A如果满足:①0A;②若对x∈A,有 ![]() ∈A,则称A是“互倒集”.给出以下数集: ①{x∈R|x2+ax+1=0}; ②{x|x2﹣4x+1<0};③{y|y=
∈A,则称A是“互倒集”.给出以下数集: ①{x∈R|x2+ax+1=0}; ②{x|x2﹣4x+1<0};③{y|y=  }.
}.
其中“互倒集”的个数是( )
A.3
B.2
C.1
D.0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 满足:f(1)=1,f(﹣2)=4.
满足:f(1)=1,f(﹣2)=4.
(1)求a,b的值,并探究是否存在常数c,使得对函数f(x)在定义域内的任意x,都有f(x)+f(c﹣x)=4成立;
(2)当x∈[1,2]时,不等式f(x)≤ ![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下判断正确的是( )
A. 命题“负数的平方是正数”不是全称命题
B. 命题“![]() ”的否定是“
”的否定是“![]() ”
”
C. “![]() ”是“函数
”是“函数![]() 的最小正周期为
的最小正周期为![]() ”的必要不充分条件
”的必要不充分条件
D. “![]() ”是“函数
”是“函数![]() 是偶函数”的充要条件
是偶函数”的充要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com