
【题目】如图,直角梯形![]() 与等腰直角三角形
与等腰直角三角形![]() 所在的平面互相垂直.
所在的平面互相垂直.![]()
![]() ,
,![]() ,
,![]() .
.
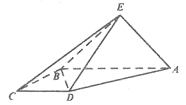
(1)求证:![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
科目:高中数学 来源: 题型:
【题目】在一次篮球投篮测试中,记分规则如下(满分为![]() 分):①每人可投篮
分):①每人可投篮![]() 次,每投中一次记
次,每投中一次记![]() 分;②若连续两次投中加
分;②若连续两次投中加![]() 分,连续三次投中加
分,连续三次投中加![]() 分,连续四次投中加
分,连续四次投中加![]() 分,以此类推,…,七次都投中加
分,以此类推,…,七次都投中加![]() 分.假设某同学每次投中的概率为
分.假设某同学每次投中的概率为![]() ,各次投篮相互独立,则:(1)该同学在测试中得
,各次投篮相互独立,则:(1)该同学在测试中得![]() 分的概率为______;(2)该同学在测试中得
分的概率为______;(2)该同学在测试中得![]() 分的概率为______..
分的概率为______..
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列叙述正确的是( )
A.相关关系是一种确定性关系,一般可分为正相关和负相关
B.回归直线一定过样本点的中心![]()
C.在回归分析中,![]() 为
为![]() 的模型比
的模型比![]() 为
为![]() 的模型拟合的效果好
的模型拟合的效果好
D.某同学研究卖出的热饮杯数![]() 与气温
与气温![]() (℃)时,一定可卖出
(℃)时,一定可卖出![]() 杯热饮
杯热饮
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列几个命题,是真命题有( )
A.若![]() ,则
,则![]()
B.若复数![]() ,
,![]() 满足
满足![]() ,则
,则![]()
C.给定两个命题![]() ,
,![]() .若
.若![]() 是
是![]() 的必要而不充分条件,则
的必要而不充分条件,则![]() 是
是![]() 的充分不必要条件
的充分不必要条件
D.命题![]() :
:![]() ,
,![]() ,
,![]() ,则
,则![]() :
:![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知三棱柱![]() 的底面是边长为2的正三角形,侧棱
的底面是边长为2的正三角形,侧棱![]() 与下底面相邻的两边AB,AC均成45度的角.
与下底面相邻的两边AB,AC均成45度的角.
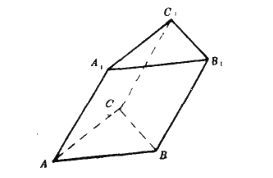
(1)求点![]() 到平面B1BCC1的距离.
到平面B1BCC1的距离.
(2)试问,当![]() 为多长时,点
为多长时,点![]() 到平面
到平面![]() 与到平面
与到平面![]() 的距离相等.
的距离相等.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)若不过原点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,与直线
两点,与直线![]() 相交于点
相交于点![]() ,且
,且![]() 是线段
是线段![]() 的中点,求
的中点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com